Documentation
¶
Documentation
¶
Overview ¶
Package gorgonia is a library that helps facilitate machine learning in Go. Write and evaluate mathematical equations involving multidimensional arrays easily. Do differentiation with them just as easily.
Example (Autodiff) ¶
Autodiff showcases automatic differentiation
g := NewGraph()
var x, y, z *Node
var err error
// define the expression
x = NewScalar(g, Float64, WithName("x"))
y = NewScalar(g, Float64, WithName("y"))
if z, err = Add(x, y); err != nil {
log.Fatal(err)
}
// set initial values then run
Let(x, 2.0)
Let(y, 2.5)
// by default, LispMachine performs forward mode and backwards mode execution
m := NewLispMachine(g)
defer m.Close()
if err = m.RunAll(); err != nil {
log.Fatal(err)
}
fmt.Printf("z: %v\n", z.Value())
if xgrad, err := x.Grad(); err == nil {
fmt.Printf("dz/dx: %v\n", xgrad)
}
if ygrad, err := y.Grad(); err == nil {
fmt.Printf("dz/dy: %v\n", ygrad)
}
Output: z: 4.5 dz/dx: 1 dz/dy: 1
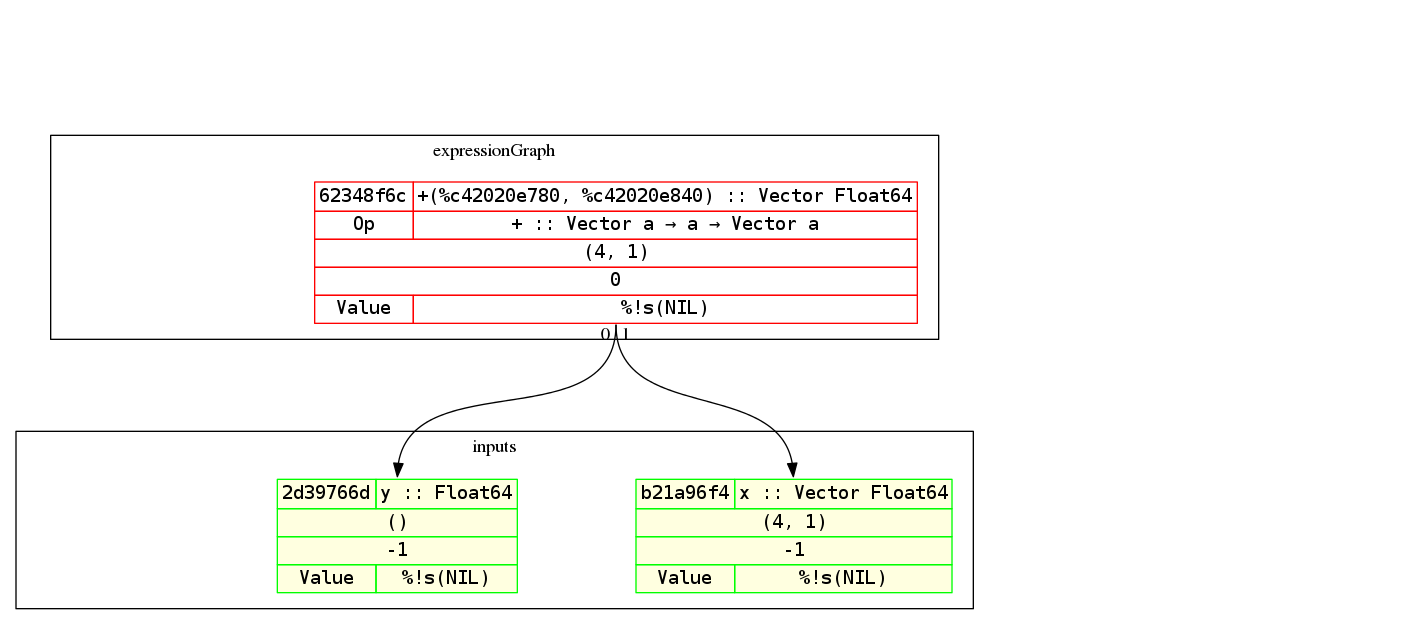
Example (Basic) ¶
Basic example of representing mathematical equations as graphs.
In this example, we want to represent the following equation
z = x + y
g := NewGraph()
var x, y, z *Node
var err error
// define the expression
x = NewScalar(g, Float64, WithName("x"))
y = NewScalar(g, Float64, WithName("y"))
if z, err = Add(x, y); err != nil {
log.Fatal(err)
}
// create a VM to run the program on
machine := NewTapeMachine(g)
defer machine.Close()
// set initial values then run
Let(x, 2.0)
Let(y, 2.5)
if err = machine.RunAll(); err != nil {
log.Fatal(err)
}
fmt.Printf("%v", z.Value())
Output: 4.5
Example (BatchedMatMul) ¶
g := NewGraph()
a := NewTensor(g, Float64, 3, WithShape(2, 2, 3), WithInit(RangedFrom(1)), WithName("a"))
b := NewTensor(g, Float64, 3, WithShape(2, 3, 2), WithInit(RangedFrom(13)), WithName("b"))
c, err := BatchedMatMul(a, b)
if err != nil {
log.Fatal(err)
}
x := NewTensor(g, Float64, 4, WithShape(3, 2, 2, 3), WithInit(RangedFrom(1)), WithName("x"))
y := NewTensor(g, Float64, 4, WithShape(3, 2, 3, 2), WithInit(RangedFrom(37)), WithName("y"))
z, err := BatchedMatMul(x, y)
if err != nil {
log.Fatal(err)
}
m := NewTapeMachine(g)
if err := m.RunAll(); err != nil {
log.Fatal(err)
}
fmt.Printf("a: %v\n%v\n", a.Value().Shape(), a.Value().Data())
fmt.Printf("b: %v\n%v\n", b.Value().Shape(), b.Value().Data())
fmt.Printf("c: %v\n%v\n", c.Value().Shape(), c.Value().Data())
fmt.Printf("x: %v\n%v\n", x.Value().Shape(), x.Value().Data())
fmt.Printf("y: %v\n%v\n", y.Value().Shape(), y.Value().Data())
fmt.Printf("z: %v\n%v\n", z.Value().Shape(), z.Value().Data())
Output: a: (2, 2, 3) [1 2 3 4 5 6 7 8 9 10 11 12] b: (2, 3, 2) [13 14 15 16 17 18 19 20 21 22 23 24] c: (2, 2, 2) [94 100 229 244 508 532 697 730] x: (3, 2, 2, 3) [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36] y: (3, 2, 3, 2) [37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72] z: (3, 2, 2, 2) [238 244 589 604 1084 1108 1489 1522 2146 2188 2605 2656 3424 3484 3937 4006 4918 4996 5485 5572 6628 6724 7249 7354]
Example (ConcurrentTraining) ¶
xV, yV, bs := prep()
concurrentTraining(xV, yV, bs, epochs)
fmt.Printf("x:\n%1.1v", xV)
fmt.Printf("y:\n%1.1v", yV)
// Outputx:
// x:
// ⎡ 6 7 8 9 ... 5e+01 5e+01 5e+01 5e+01⎤
// ⎢7e+01 7e+01 7e+01 7e+01 ... 1e+02 1e+02 1e+02 1e+02⎥
// ⎢1e+02 1e+02 1e+02 1e+02 ... 2e+02 2e+02 2e+02 2e+02⎥
// ⎢2e+02 2e+02 2e+02 2e+02 ... 2e+02 2e+02 2e+02 2e+02⎥
// .
// .
// .
// ⎢4e+07 4e+07 4e+07 4e+07 ... 4e+07 4e+07 4e+07 4e+07⎥
// ⎢4e+07 4e+07 4e+07 4e+07 ... 4e+07 4e+07 4e+07 4e+07⎥
// ⎢4e+07 4e+07 4e+07 4e+07 ... 4e+07 4e+07 4e+07 4e+07⎥
// ⎣4e+07 4e+07 4e+07 4e+07 ... 4e+07 4e+07 4e+07 4e+07⎦
// y:
// [-1e+02 -4e+02 -7e+02 -9e+02 ... -2e+08 -2e+08 -2e+08 -2e+08]
Output:
Example (ErrorHandling) ¶
Gorgonia provides an API that is fairly idiomatic - most of the functions in in the API return (T, error). This is useful for many cases, such as an interactive shell for deep learning. However, it must also be acknowledged that this makes composing functions together a bit cumbersome.
To that end, Gorgonia provides two alternative methods. First, the `Lift` based functions; Second the `Must` function
// Lift
g := NewGraph()
x := NewMatrix(g, Float32, WithShape(2, 3), WithInit(RangedFrom(0)), WithName("a"))
y := NewMatrix(g, Float32, WithShape(3, 2), WithInit(ValuesOf(float32(2))), WithName("b"))
z := NewMatrix(g, Float32, WithShape(2, 1), WithInit(Zeroes()), WithName("bias"))
wrong := NewMatrix(g, Float64, WithShape(2, 3), WithInit(RangedFrom(0)), WithName("wrong"))
// Different LiftXXX functions exist for different API signatures
// A good way to do this is to have some instantiated functions at the top level of the package
mul := Lift2(Mul)
add := Lift2(Add)
addB := Lift2Broadcast(BroadcastAdd)
sq := Lift1(Square)
sm := Lift1Axial(SoftMax)
nn := sm(sq(addB(mul(x, y), z, nil, []byte{1}))) // OK
nnPlusWrong := add(nn, wrong) // Wrong types. Will Error
fmt.Printf("nn: %v\nAn error occurs: %v\n", nn, nnPlusWrong.Err())
// Must()
h := NewGraph()
a := NewMatrix(h, Float32, WithShape(2, 3), WithInit(RangedFrom(0)), WithName("a"))
b := NewMatrix(h, Float32, WithShape(3, 2), WithInit(ValuesOf(float32(2))), WithName("b"))
c := NewMatrix(h, Float32, WithShape(2, 1), WithInit(RangedFrom(0)), WithName("c"))
wrong2 := NewMatrix(h, Float64, WithShape(2, 3), WithInit(RangedFrom(0)), WithName("wrong"))
// This is OK
nn2 := Must(SoftMax(
Must(Square(
Must(BroadcastAdd(
Must(Mul(a, b)),
c,
nil, []byte{1},
)),
)),
))
fmt.Printf("nn2: %v\n", nn2)
defer func() {
if r := recover(); r != nil {
fmt.Printf("An error occurs (caught by recover()): %v\n", r)
}
}()
nn2PlusWrong := Must(Add(nn2, wrong2))
_ = nn2PlusWrong
Output: nn: ÷ false(%9, %d) :: Matrix float32 An error occurs: Type inference error. Op: + false. Children: [Matrix float32, Matrix float64], OpType:Matrix a → Matrix a → Matrix a: Unable to unify while inferring type of + false: Unification Fail: float64 ~ float32 cannot be unified nn2: ÷ false(%9, %d) :: Matrix float32 An error occurs (caught by recover()): Type inference error. Op: + false. Children: [Matrix float32, Matrix float64], OpType:Matrix a → Matrix a → Matrix a: Unable to unify while inferring type of + false: Unification Fail: float64 ~ float32 cannot be unified
Example (KeepDims) ¶
g := NewGraph()
a := NodeFromAny(g, tensor.New(tensor.WithShape(2, 3), tensor.WithBacking([]float64{1, 2, 3, 4, 5, 6})))
m1, _ := Mean(a, 1)
m2, _ := KeepDims(a, false, func(a *Node) (*Node, error) { return Mean(a, 1) })
m3, _ := Mean(a, 0)
m4, _ := KeepDims(a, true, func(a *Node) (*Node, error) { return Mean(a, 0) })
_, err := KeepDims(a, true, func(a *Node) (*Node, error) { return Mean(a) })
if err == nil {
panic("expected an error: you can't keep dims on a scalar result")
}
vm := NewTapeMachine(g)
if err := vm.RunAll(); err != nil {
panic(err)
}
fmt.Printf("a:\n%v\n", a.Value())
fmt.Printf("m1 (shape: %v):\n%v\n", m1.Value().Shape(), m1.Value())
fmt.Printf("m2 (shape: %v):\n%v\n", m2.Value().Shape(), m2.Value())
fmt.Printf("m3 (shape: %v):\n%v\n", m3.Value().Shape(), m3.Value())
fmt.Printf("m4 (shape: %v):\n%v\n", m4.Value().Shape(), m4.Value())
Output: a: ⎡1 2 3⎤ ⎣4 5 6⎦ m1 (shape: (2)): [2 5] m2 (shape: (2, 1)): C[2 5] m3 (shape: (3)): [2.5 3.5 4.5] m4 (shape: (1, 3)): R[2.5 3.5 4.5]
Example (LinearRegression) ¶
Linear Regression Example
The formula for a straight line is
y = mx + c
We want to find an `m` and a `c` that fits the equation well. We'll do it in both float32 and float64 to showcase the extensibility of Gorgonia
package main
import (
"fmt"
"log"
"math/rand"
"runtime"
. "gorgonia.org/gorgonia"
"gorgonia.org/tensor"
)
const (
vecSize = 1000000
)
// manually generate a fake dataset which is y=2x+random
func xy(dt tensor.Dtype) (x tensor.Tensor, y tensor.Tensor) {
var xBack, yBack interface{}
switch dt {
case Float32:
xBack = tensor.Range(tensor.Float32, 1, vecSize+1).([]float32)
yBackC := tensor.Range(tensor.Float32, 1, vecSize+1).([]float32)
for i, v := range yBackC {
yBackC[i] = v*2 + rand.Float32()
}
yBack = yBackC
case Float64:
xBack = tensor.Range(tensor.Float64, 1, vecSize+1).([]float64)
yBackC := tensor.Range(tensor.Float64, 1, vecSize+1).([]float64)
for i, v := range yBackC {
yBackC[i] = v*2 + rand.Float64()
}
yBack = yBackC
}
x = tensor.New(tensor.WithBacking(xBack), tensor.WithShape(vecSize))
y = tensor.New(tensor.WithBacking(yBack), tensor.WithShape(vecSize))
return
}
func random(dt tensor.Dtype) interface{} {
rand.Seed(13370)
switch dt {
case tensor.Float32:
return rand.Float32()
case tensor.Float64:
return rand.Float64()
default:
panic("Unhandled dtype")
}
}
func linregSetup(Float tensor.Dtype) (m, c *Node, machine VM) {
var xT, yT Value
xT, yT = xy(Float)
g := NewGraph()
x := NewVector(g, Float, WithShape(vecSize), WithName("x"), WithValue(xT))
y := NewVector(g, Float, WithShape(vecSize), WithName("y"), WithValue(yT))
m = NewScalar(g, Float, WithName("m"), WithValue(random(Float)))
c = NewScalar(g, Float, WithName("c"), WithValue(random(Float)))
pred := Must(Add(Must(Mul(x, m)), c))
se := Must(Square(Must(Sub(pred, y))))
cost := Must(Mean(se))
if _, err := Grad(cost, m, c); err != nil {
log.Fatalf("Failed to backpropagate: %v", err)
}
// machine := NewLispMachine(g) // you can use a LispMachine, but it'll be VERY slow.
machine = NewTapeMachine(g, BindDualValues(m, c))
return m, c, machine
}
func linregRun(m, c *Node, machine VM, iter int, autoCleanup bool) (retM, retC Value) {
if autoCleanup {
defer machine.Close()
}
model := []ValueGrad{m, c}
solver := NewVanillaSolver(WithLearnRate(0.001), WithClip(5)) // good idea to clip
if CUDA {
runtime.LockOSThread()
defer runtime.UnlockOSThread()
}
var err error
for i := 0; i < iter; i++ {
if err = machine.RunAll(); err != nil {
fmt.Printf("Error during iteration: %v: %v\n", i, err)
break
}
if err = solver.Step(model); err != nil {
log.Fatal(err)
}
machine.Reset() // Reset is necessary in a loop like this
}
return m.Value(), c.Value()
}
func linearRegression(Float tensor.Dtype, iter int) (retM, retC Value) {
defer runtime.GC()
m, c, machine := linregSetup(Float)
return linregRun(m, c, machine, iter, true)
}
// Linear Regression Example
//
// The formula for a straight line is
//
// y = mx + c
//
// We want to find an `m` and a `c` that fits the equation well. We'll do it in both float32 and float64 to showcase the extensibility of Gorgonia
func main() {
var m, c Value
// Float32
m, c = linearRegression(Float32, 500)
fmt.Printf("float32: y = %3.3fx + %3.3f\n", m, c)
// Float64
m, c = linearRegression(Float64, 500)
fmt.Printf("float64: y = %3.3fx + %3.3f\n", m, c)
}
Output: float32: y = 2.001x + 2.001 float64: y = 2.001x + 2.001
Example (NonConcurrentTraining) ¶
xV, yV, _ := prep()
nonConcurrentTraining(xV, yV, epochs)
fmt.Printf("x:\n%1.1v", xV)
fmt.Printf("y:\n%1.1v", yV)
Output: x: ⎡ 6 7 8 9 ... 5e+01 5e+01 5e+01 5e+01⎤ ⎢7e+01 7e+01 7e+01 7e+01 ... 1e+02 1e+02 1e+02 1e+02⎥ ⎢1e+02 1e+02 1e+02 1e+02 ... 2e+02 2e+02 2e+02 2e+02⎥ ⎢2e+02 2e+02 2e+02 2e+02 ... 2e+02 2e+02 2e+02 2e+02⎥ . . . ⎢4e+07 4e+07 4e+07 4e+07 ... 4e+07 4e+07 4e+07 4e+07⎥ ⎢4e+07 4e+07 4e+07 4e+07 ... 4e+07 4e+07 4e+07 4e+07⎥ ⎢4e+07 4e+07 4e+07 4e+07 ... 4e+07 4e+07 4e+07 4e+07⎥ ⎣4e+07 4e+07 4e+07 4e+07 ... 4e+07 4e+07 4e+07 4e+07⎦ y: [-1e+02 -4e+02 -7e+02 -9e+02 ... -2e+08 -2e+08 -2e+08 -2e+08]
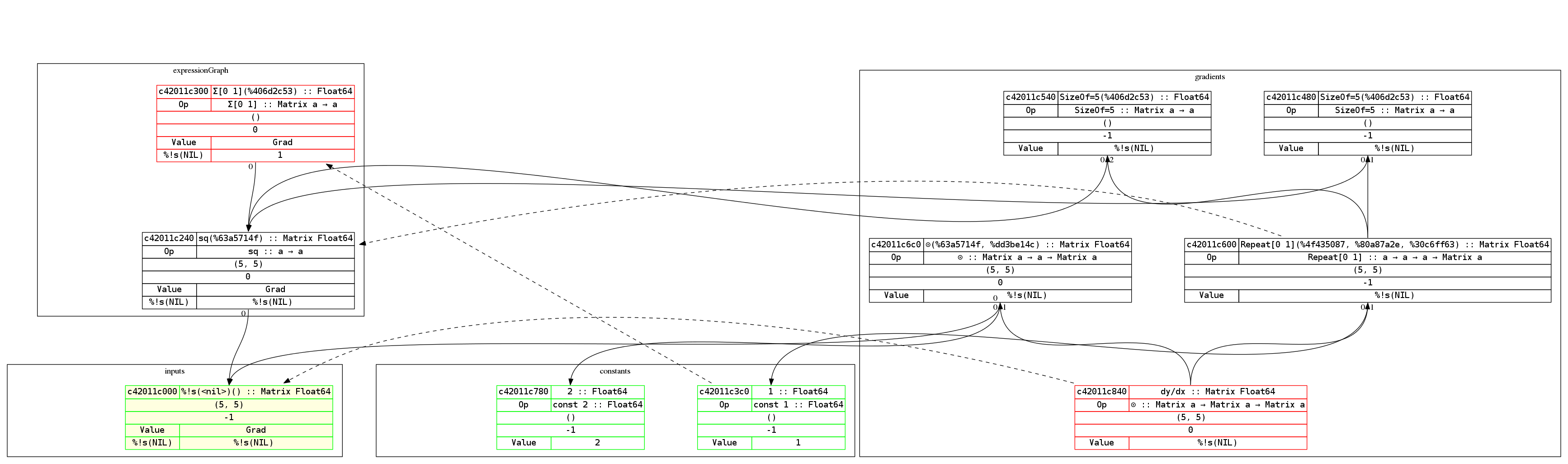
Example (SymbolicDiff) ¶
SymbolicDiff showcases symbolic differentiation
g := NewGraph()
var x, y, z *Node
var err error
// define the expression
x = NewScalar(g, Float64, WithName("x"))
y = NewScalar(g, Float64, WithName("y"))
if z, err = Add(x, y); err != nil {
log.Fatal(err)
}
// symbolically differentiate z with regards to x and y
// this adds the gradient nodes to the graph g
var grads Nodes
if grads, err = Grad(z, x, y); err != nil {
log.Fatal(err)
}
// create a VM to run the program on
machine := NewTapeMachine(g)
defer machine.Close()
// set initial values then run
Let(x, 2.0)
Let(y, 2.5)
if err = machine.RunAll(); err != nil {
log.Fatal(err)
}
fmt.Printf("z: %v\n", z.Value())
if xgrad, err := x.Grad(); err == nil {
fmt.Printf("dz/dx: %v | %v\n", xgrad, grads[0].Value())
}
if ygrad, err := y.Grad(); err == nil {
fmt.Printf("dz/dy: %v | %v\n", ygrad, grads[1].Value())
}
Output: z: 4.5 dz/dx: 1 | 1 dz/dy: 1 | 1
Index ¶
- Constants
- Variables
- func BatchNorm(x, scale, bias *Node, momentum, epsilon float64) (retVal, γ, β *Node, op *BatchNormOp, err error)
- func Binomial32(trials, prob float64, s ...int) []float32
- func Binomial64(trials, prob float64, s ...int) []float64
- func Broadcast(a, b *Node, pattern BroadcastPattern) (*Node, *Node, error)
- func CheckOne(in Input) error
- func Compile(g *ExprGraph) (prog *program, locMap map[*Node]register, err error)
- func CompileFunction(g *ExprGraph, inputs, outputs Nodes) (prog *program, locMap map[*Node]register, err error)
- func DebugDerives()
- func DimSizersToShapes(ds []DimSizer) ([]tensor.Shape, error)
- func DontDebugDerives()
- func FmtNodeMap(m interface{}) mapFmt
- func Gaussian32(mean, stdev float64, s ...int) []float32
- func Gaussian64(mean, stdev float64, s ...int) []float64
- func GlorotEtAlN32(gain float64, s ...int) []float32
- func GlorotEtAlN64(gain float64, s ...int) []float64
- func GlorotEtAlU32(gain float64, s ...int) []float32
- func GlorotEtAlU64(gain float64, s ...int) []float64
- func GraphCollisionStats() (int, int, int)
- func HeEtAlN64(gain float64, s ...int) []float64
- func HeEtAlU64(gain float64, s ...int) []float64
- func Let(n *Node, be interface{}) error
- func Lift1(fn func(a *Node) (*Node, error)) func(a Input) Result
- func Lift1Axial(fn func(a *Node, axes ...int) (*Node, error)) func(a Input, axes ...int) Result
- func Lift2(fn func(a, b *Node) (*Node, error)) func(a, b Input) Result
- func Lift2Broadcast(fn func(a, b *Node, pat1, pat2 []byte) (*Node, error)) func(a, b Input, pat1, pat2 []byte) Result
- func NewLispMachine(g *ExprGraph, opts ...VMOpt) *lispMachine
- func NewTapeMachine(g *ExprGraph, opts ...VMOpt) *tapeMachine
- func ReturnNode(n *Node)
- func ReturnType(t hm.Type)
- func S(start int, opt ...int) tensor.Slice
- func SetDerivOf(deriv, of *Node)
- func SetOptimizationLevel(i int)
- func TypeOf(v Value) hm.Type
- func Uniform32(low, high float64, s ...int) []float32
- func Uniform64(low, high float64, s ...int) []float64
- func UnsafeLet(n *Node, be interface{}) error
- func Use(b BLAS)
- func UseNonStable()
- func UseStabilization()
- func ValueClose(a, b Value) bool
- func ValueEq(a, b Value) bool
- func WalkGraph(start *Node) <-chan *Node
- func WithGraphName(name string) graphconopt
- type ADOp
- type AdaGradSolver
- type AdamSolver
- type Arena
- type AutoDiffError
- type B
- type BLAS
- type BarzilaiBorweinSolver
- type BatchNormOp
- func (op *BatchNormOp) Arity() int
- func (op *BatchNormOp) CallsExtern() bool
- func (op *BatchNormOp) DiffWRT(inputs int) []bool
- func (op *BatchNormOp) Do(values ...Value) (retVal Value, err error)
- func (op *BatchNormOp) DoDiff(ctx ExecutionContext, inputs Nodes, output *Node) error
- func (op *BatchNormOp) Hashcode() uint32
- func (op *BatchNormOp) InferShape(ns ...DimSizer) (tensor.Shape, error)
- func (op *BatchNormOp) OverwritesInput() int
- func (op *BatchNormOp) Reset() error
- func (op *BatchNormOp) ReturnsPtr() bool
- func (op *BatchNormOp) SetTesting()
- func (op *BatchNormOp) SetTraining()
- func (op *BatchNormOp) String() string
- func (op *BatchNormOp) SymDiff(inputs Nodes, output *Node, grad *Node) (retVal Nodes, err error)
- func (op *BatchNormOp) Type() hm.Type
- func (op *BatchNormOp) UsePreallocDo(prealloc Value, inputs ...Value) (retVal Value, err error)
- func (op *BatchNormOp) WriteHash(h hash.Hash)
- type Batched
- type BatchedBLAS
- type BatchedDevice
- type BinaryOp
- type BroadcastPattern
- type CLDoer
- type CUDAADOp
- type CUDADoer
- type CloneErrorer
- type Cloner
- type CopierFrom
- type CopierTo
- type Device
- type DimSizer
- type Dtyper
- type Err
- type Errer
- type ExecutionContext
- type ExprGraph
- func (g *ExprGraph) AddNode(n *Node) (retVal *Node)
- func (g *ExprGraph) AllNodes() Nodes
- func (g *ExprGraph) ByName(name string) (retVal Nodes)
- func (g *ExprGraph) Clone() interface{}
- func (g *ExprGraph) Constant(v Value) *Node
- func (g *ExprGraph) Edge(u, v int64) graph.Edge
- func (g *ExprGraph) Edges() graph.Edges
- func (g *ExprGraph) ExactSubgraphRoots(ns ...*Node) *ExprGraph
- func (g *ExprGraph) From(nodeid int64) graph.Nodes
- func (g *ExprGraph) Has(nodeid int64) bool
- func (g *ExprGraph) HasEdgeBetween(x, y int64) bool
- func (g *ExprGraph) HasEdgeFromTo(u, v int64) bool
- func (g *ExprGraph) Inputs() (retVal Nodes)
- func (g *ExprGraph) Node(id int64) graph.Node
- func (g *ExprGraph) Nodes() graph.Nodes
- func (g *ExprGraph) RemoveNode(node graph.Node)
- func (g *ExprGraph) Roots() (retVal Nodes)
- func (g *ExprGraph) SetEdge(e graph.Edge)
- func (g *ExprGraph) String() string
- func (g *ExprGraph) Subgraph(ns ...*Node) *ExprGraph
- func (g *ExprGraph) SubgraphRoots(ns ...*Node) *ExprGraph
- func (g *ExprGraph) To(nid int64) graph.Nodes
- func (g *ExprGraph) ToDot() string
- func (g *ExprGraph) UnbindAll()
- func (g *ExprGraph) UnbindAllNonInputs()
- type ExternMetadata
- func (m *ExternMetadata) Cleanup()
- func (m *ExternMetadata) DoWork() error
- func (m *ExternMetadata) Get(dev Device, size int64) (tensor.Memory, error)
- func (m *ExternMetadata) GetFromValue(dev Device, v Value) (tensor.Memory, error)
- func (m ExternMetadata) HasFunc(name string) bool
- func (m *ExternMetadata) Put(dev Device, mem tensor.Memory, size int64)
- func (m *ExternMetadata) PutValue(dev Device, v Value)
- func (m *ExternMetadata) Reset()
- func (m *ExternMetadata) Signal()
- func (m *ExternMetadata) Sync() chan struct{}
- func (m *ExternMetadata) Transfer(toDev, fromDev Device, v Value, synchronous bool) (retVal Value, err error)
- func (m *ExternMetadata) WorkAvailable() <-chan bool
- type External
- type ExternalOp
- type F32
- type F64
- type I
- type I32
- type I64
- type IncrDoer
- type InitWFn
- func Gaussian(mean, stdev float64) InitWFn
- func GlorotN(gain float64) InitWFn
- func GlorotU(gain float64) InitWFn
- func HeN(gain float64) InitWFn
- func HeU(gain float64) InitWFn
- func Ones() InitWFn
- func RangedFrom(start int) InitWFn
- func Uniform(low, high float64) InitWFn
- func ValuesOf(val interface{}) InitWFn
- func Zeroes() InitWFn
- type Input
- type Momentum
- type Namer
- type NoOpError
- type NoRetOp
- type Node
- func Abs(a *Node) (*Node, error)
- func Add(a, b *Node) (*Node, error)
- func ApplyOp(op Op, children ...*Node) (retVal *Node, err error)
- func ApplyOpWithName(op Op, name string, children ...*Node) (retVal *Node, err error)
- func At(a *Node, coords ...int) (retVal *Node, err error)
- func BatchedMatMul(a, b *Node, transes ...bool) (retVal *Node, err error)
- func BinaryXent(output, target *Node) (retVal *Node, err error)
- func BinomialRandomNode(g *ExprGraph, dt tensor.Dtype, trials, prob float64, shape ...int) *Node
- func BroadcastAdd(a, b *Node, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastEq(a, b *Node, retSame bool, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastGt(a, b *Node, retSame bool, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastGte(a, b *Node, retSame bool, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastHadamardDiv(a, b *Node, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastHadamardProd(a, b *Node, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastLt(a, b *Node, retSame bool, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastLte(a, b *Node, retSame bool, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastNe(a, b *Node, retSame bool, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastPow(a, b *Node, leftPattern, rightPattern []byte) (*Node, error)
- func BroadcastSub(a, b *Node, leftPattern, rightPattern []byte) (*Node, error)
- func Ceil(a *Node) (*Node, error)
- func Concat(axis int, ns ...*Node) (retVal *Node, err error)
- func Conv1d(in, filter *Node, kernel, pad, stride, dilation int) (*Node, error)
- func Conv2d(im, filter *Node, kernelShape tensor.Shape, pad, stride, dilation []int) (retVal *Node, err error)
- func Cos(a *Node) (*Node, error)
- func Cube(a *Node) (*Node, error)
- func Div(a, b *Node) (retVal *Node, err error)
- func Dropout(x *Node, prob float64) (retVal *Node, err error)
- func Eq(a, b *Node, retSame bool) (*Node, error)
- func Exp(a *Node) (*Node, error)
- func Expm1(a *Node) (*Node, error)
- func Floor(a *Node) (*Node, error)
- func GaussianRandomNode(g *ExprGraph, dt tensor.Dtype, mean, stdev float64, shape ...int) *Node
- func GlobalAveragePool2D(x *Node) (*Node, error)
- func Gt(a, b *Node, retSame bool) (*Node, error)
- func Gte(a, b *Node, retSame bool) (*Node, error)
- func HadamardDiv(a, b *Node) (*Node, error)
- func HadamardProd(a, b *Node) (*Node, error)
- func Im2Col(n *Node, kernel, pad, stride, dilation tensor.Shape) (retVal *Node, err error)
- func Inverse(a *Node) (*Node, error)
- func InverseSqrt(a *Node) (*Node, error)
- func KeepDims(a *Node, expandLeft bool, fn func(a *Node) (*Node, error)) (*Node, error)
- func LeakyRelu(x *Node, alpha float64) (*Node, error)
- func Log(a *Node) (*Node, error)
- func Log1p(a *Node) (*Node, error)
- func Log2(a *Node) (*Node, error)
- func LogSumExp(a *Node, axis int) (retVal *Node, err error)
- func Lt(a, b *Node, retSame bool) (*Node, error)
- func Lte(a, b *Node, retSame bool) (*Node, error)
- func Max(a *Node, along ...int) (retVal *Node, err error)
- func MaxPool1D(x *Node, kernel, pad, stride int) (*Node, error)
- func MaxPool2D(x *Node, kernel tensor.Shape, pad, stride []int) (*Node, error)
- func Mean(a *Node, along ...int) (retVal *Node, err error)
- func Mul(a, b *Node) (retVal *Node, err error)
- func Must(n *Node, err error, opts ...NodeConsOpt) *Node
- func Ne(a, b *Node, retSame bool) (*Node, error)
- func Neg(a *Node) (*Node, error)
- func NegNegOptimization(a *Node) (retVal *Node, err error)
- func NewConstant(v interface{}, opts ...NodeConsOpt) *Node
- func NewMatrix(g *ExprGraph, t tensor.Dtype, opts ...NodeConsOpt) *Node
- func NewScalar(g *ExprGraph, t tensor.Dtype, opts ...NodeConsOpt) *Node
- func NewTensor(g *ExprGraph, t tensor.Dtype, dims int, opts ...NodeConsOpt) *Node
- func NewUniqueNode(opts ...NodeConsOpt) *Node
- func NewVector(g *ExprGraph, t tensor.Dtype, opts ...NodeConsOpt) *Node
- func NodeFromAny(g *ExprGraph, any interface{}, opts ...NodeConsOpt) *Node
- func Norm(a *Node, axis, p int) (retVal *Node, err error)
- func OneHotVector(id, classes int, t tensor.Dtype, opts ...NodeConsOpt) *Node
- func OuterProd(a, b *Node) (retVal *Node, err error)
- func Pow(a, b *Node) (*Node, error)
- func Read(n *Node, into *Value) (retVal *Node)
- func Rectify(x *Node) (retVal *Node, err error)
- func ReduceAdd(nodes Nodes, opts ...NodeConsOpt) (retVal *Node, err error)
- func ReduceMul(nodes Nodes, opts ...NodeConsOpt) (retVal *Node, err error)
- func Reshape(n *Node, to tensor.Shape) (retVal *Node, err error)
- func Set(a, b *Node) (retVal *Node)
- func Sigmoid(a *Node) (*Node, error)
- func Sign(a *Node) (*Node, error)
- func Sin(a *Node) (*Node, error)
- func SizeOf(axis int, x *Node) (retVal *Node, err error)
- func Slice(n *Node, slices ...tensor.Slice) (retVal *Node, err error)
- func SoftMax(a *Node, axes ...int) (retVal *Node, err error)
- func Softplus(a *Node) (*Node, error)
- func Sqrt(a *Node) (*Node, error)
- func Square(a *Node) (*Node, error)
- func StableSoftMax(a *Node) (retVal *Node, err error)
- func Sub(a, b *Node) (*Node, error)
- func Sum(a *Node, along ...int) (retVal *Node, err error)
- func Tanh(a *Node) (*Node, error)
- func Tensordot(aAxes []int, bAxes []int, a, b *Node) (retVal *Node, err error)
- func Transpose(n *Node, axes ...int) (retVal *Node, err error)
- func UniformRandomNode(g *ExprGraph, dt tensor.Dtype, low, high float64, shape ...int) *Node
- func (n *Node) Clone() (retVal interface{})
- func (n *Node) CloneTo(g *ExprGraph) *Node
- func (n *Node) DataSize() int
- func (n *Node) Device() Device
- func (n *Node) Dims() int
- func (n *Node) Dtype() tensor.Dtype
- func (n *Node) Err() error
- func (n *Node) Grad() (Value, error)
- func (n *Node) GradOnDevice(dev Device, extern External) (retVal Value, allocOnExtern bool, err error)
- func (n *Node) Graph() *ExprGraph
- func (n *Node) Groups() encoding.Groups
- func (n *Node) Hashcode() uint32
- func (n *Node) ID() int64
- func (n *Node) IsColVec() bool
- func (n *Node) IsMatrix() bool
- func (n *Node) IsRowVec() bool
- func (n *Node) IsScalar() bool
- func (n *Node) IsVar() bool
- func (n *Node) IsVec() bool
- func (n *Node) IsVector() bool
- func (n *Node) Name() string
- func (n *Node) Node() *Node
- func (n *Node) Nodes() Nodes
- func (n *Node) Op() Op
- func (n *Node) RestrictedToDot(up, down int) string
- func (n *Node) Shape() tensor.Shape
- func (n *Node) Strides() []int
- func (n *Node) String() string
- func (n *Node) ToDot() string
- func (n *Node) Type() hm.Type
- func (n *Node) Value() Value
- func (n *Node) ValueOnDevice(dev Device, extern External) (retVal Value, allocOnExtern bool, err error)
- func (n *Node) WriteHash(h hash.Hash32)
- type NodeConsOpt
- func In(g *ExprGraph) NodeConsOpt
- func WithChildren(children Nodes) NodeConsOpt
- func WithGrad(any interface{}) NodeConsOpt
- func WithGroupName(name string) NodeConsOpt
- func WithInit(fn InitWFn) NodeConsOpt
- func WithName(name string) NodeConsOpt
- func WithOp(op Op) NodeConsOpt
- func WithShape(shp ...int) NodeConsOpt
- func WithType(t hm.Type) NodeConsOpt
- func WithValue(any interface{}) NodeConsOpt
- type NodeSet
- func (set NodeSet) Add(i *Node) bool
- func (set NodeSet) Cardinality() int
- func (set *NodeSet) Clear()
- func (set NodeSet) Clone() NodeSet
- func (set NodeSet) Contains(i *Node) bool
- func (set NodeSet) ContainsAll(i ...*Node) bool
- func (set NodeSet) Difference(other NodeSet) NodeSet
- func (set NodeSet) Equal(other NodeSet) bool
- func (set NodeSet) Intersect(other NodeSet) NodeSet
- func (set NodeSet) IsSubset(other NodeSet) bool
- func (set NodeSet) IsSuperset(other NodeSet) bool
- func (set NodeSet) Iter() <-chan *Node
- func (set NodeSet) Remove(i *Node)
- func (set NodeSet) SymmetricDifference(other NodeSet) NodeSet
- func (set NodeSet) ToSlice() Nodes
- func (set NodeSet) Union(other NodeSet) NodeSet
- type Nodes
- func Backpropagate(outputs, gradOutputs, wrt Nodes) (retVal Nodes, err error)
- func Grad(cost *Node, WRTs ...*Node) (retVal Nodes, err error)
- func NodesFromInputs(xs ...Input) (Nodes, error)
- func Sort(g *ExprGraph) (sorted Nodes, err error)
- func Unconcat(a *Node, along int, n int) (Nodes, error)
- func UnstableSort(g *ExprGraph) (sorted Nodes, err error)
- func (ns Nodes) Add(n *Node) Nodes
- func (ns Nodes) AllSameGraph() bool
- func (ns Nodes) Contains(want *Node) bool
- func (ns Nodes) Difference(other Nodes) Nodes
- func (ns Nodes) Equals(other Nodes) bool
- func (ns Nodes) Err() error
- func (ns Nodes) Format(s fmt.State, c rune)
- func (ns Nodes) Intersect(other Nodes) Nodes
- func (ns Nodes) Len() int
- func (ns Nodes) Less(i, j int) bool
- func (ns Nodes) Node() *Node
- func (ns Nodes) Nodes() Nodes
- func (ns Nodes) Set() Nodes
- func (ns Nodes) Swap(i, j int)
- type Op
- type RMSPropSolver
- type ReductionOp
- type Result
- type SDOp
- type Scalar
- type Solver
- type SolverOpt
- func WithBatchSize(batch float64) SolverOpt
- func WithBeta1(beta1 float64) SolverOpt
- func WithBeta2(beta2 float64) SolverOpt
- func WithClip(clip float64) SolverOpt
- func WithEps(eps float64) SolverOpt
- func WithL1Reg(l1reg float64) SolverOpt
- func WithL2Reg(l2reg float64) SolverOpt
- func WithLearnRate(eta float64) SolverOpt
- func WithMomentum(momentum float64) SolverOpt
- func WithRho(rho float64) SolverOpt
- type StandardEngine
- type SymDiffError
- type Tensor
- type TensorType
- func (t TensorType) Apply(sub hm.Subs) hm.Substitutable
- func (t TensorType) Eq(other hm.Type) bool
- func (t TensorType) Format(state fmt.State, c rune)
- func (t TensorType) FreeTypeVar() hm.TypeVarSet
- func (t TensorType) Name() string
- func (t TensorType) Normalize(k, v hm.TypeVarSet) (hm.Type, error)
- func (t TensorType) String() string
- func (t TensorType) Types() hm.Types
- type Typer
- type U8
- type UnaryOp
- type UnsafeDoer
- type UsePreallocDoer
- type VM
- type VMOpt
- func BindDualValues(nodes ...*Node) VMOpt
- func ExecuteBwdOnly() VMOpt
- func ExecuteFwdOnly() VMOpt
- func LogBothDir() VMOpt
- func LogBwd() VMOpt
- func LogFwd() VMOpt
- func TraceExec() VMOpt
- func UseCudaFor(ops ...string) VMOpt
- func WithEngine(e tensor.Engine) VMOpt
- func WithInfWatch() VMOpt
- func WithLogger(logger *log.Logger) VMOpt
- func WithManualGradient() VMOpt
- func WithNaNWatch() VMOpt
- func WithPrecompiled(prog *program, locMap map[*Node]register) VMOpt
- func WithValueFmt(format string) VMOpt
- func WithWatchlist(list ...interface{}) VMOpt
- type Value
- type ValueCloser
- type ValueEqualer
- type ValueGrad
- type Valuer
- type VanillaSolver
- type ZeroValuer
- type Zeroer
Examples ¶
Constants ¶
const CUDA = false
CUDA indicates if this build is using CUDA
const DEBUG = false
DEBUG indicates if this build is in debug mode. It is not.
Variables ¶
var ( // Float64 ... Float64 = tensor.Float64 // Float32 ... Float32 = tensor.Float32 // Int ... Int = tensor.Int // Int64 ... Int64 = tensor.Int64 // Int32 ... Int32 = tensor.Int32 // Byte ... Byte = tensor.Uint8 // Bool ... Bool = tensor.Bool // Ptr is equivalent to interface{}. Ugh Ugh Ugh Ptr = tensor.UnsafePointer )
Functions ¶
func BatchNorm ¶
func BatchNorm(x, scale, bias *Node, momentum, epsilon float64) (retVal, γ, β *Node, op *BatchNormOp, err error)
BatchNorm applies a batchnormalization. This operator can be used in forward pass or for training. In an evaluation only, the "op" output can be discared. In training phase, γ, β can be discarded and the op should be used.
func Binomial32 ¶
Binomial32 returns a []float32 drawn from a binomial distribution given the trial and probability parameters.
func Binomial64 ¶
Binomial64 returns a []float64 drawn from a binomial distribution given the trial and probability parameters.
func Broadcast ¶
func Broadcast(a, b *Node, pattern BroadcastPattern) (*Node, *Node, error)
Broadcast apply the pattern to the input nodes and returns two nodes suitable for a binary operator. Broadcast works somewhat like Numpy's broadcast, except it's now exposed as a function.
func CompileFunction ¶
func CompileFunction(g *ExprGraph, inputs, outputs Nodes) (prog *program, locMap map[*Node]register, err error)
CompileFunction takes a graph, subsets it based on the input and output nodes provided and outputs a program suitable for *tapeMachine to run. It is analogous to theano.Function(). If some input nodes are not used or is not reachable, this function will return an error
func DebugDerives ¶
func DebugDerives()
DebugDerives turns on the derivation debug option when printing a graph
func DimSizersToShapes ¶
DimSizersToShapes is a convenience function to convert a slice of DimSizer to a slice of tensor.Shape. It will return an error if any of them isn't a tensor.Shape
func DontDebugDerives ¶
func DontDebugDerives()
DontDebugDerives turns off derivation debug option when printing a graph. It is off by default
func FmtNodeMap ¶
func FmtNodeMap(m interface{}) mapFmt
FmtNodeMap is a convenience function to print map[*Node]<T>
The fmt flag that makes it all nicely formatted is "-". Because a map consists of two types (key's type and val's type), and the Go fmt verb doesn't quite allow us to do something like "%ds", a hack is introduced to enable nicer printing of map[*Node]<T>
Here's the hack: The "#" flag is used to indicate if the map will use the Node's ID or Name when formatting the map.
%-v nodeName:%v %-#v nodeID:%v %-d nodeName:%x %-#d nodeID: %x %-p nodeName:%p %-#p nodeID:%p
If the "-" flag is not found, then the formatter returns the default Go format for map[<T>]<T2>
func Gaussian32 ¶
Gaussian32 returns a []float32 drawn from a gaussian distribution as defined by the mean and stdev
func Gaussian64 ¶
Gaussian64 returns a []float64 drawn from a gaussian distribution as defined by the mean and stdev
func GlorotEtAlN32 ¶
GlorotEtAlN32 returns float32 weights sampled from a normal distribution using the methods specified in Glorot et. al (2010). See also: http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
func GlorotEtAlN64 ¶
GlorotEtAlN64 returns float64 weights sampled from a normal distribution using the methods specified in Glorot et. al (2010). See also: http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
func GlorotEtAlU32 ¶
GlorotEtAlU32 returns float32 weights sampled from a uniform distribution using the methods specified in Glorot et. al (2010). See also: http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
For best results, use:
1.0 for gain for weights that will be used in linear and/or sigmoid units math.Sqrt(2.0) for gain for weights that will be used in ReLU units math.Sqrt(2.0 / (1+alpha*alpha)) for ReLU that are leaky with alpha
func GlorotEtAlU64 ¶
GlorotEtAlU64 returns float64 weights sampled from a uniform distribution using the methods specified in Glorot et. al (2010). See also: http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
For best results, use:
1.0 for gain for weights that will be used in linear and/or sigmoid units math.Sqrt(2.0) for gain for weights that will be used in ReLU units math.Sqrt(2.0 / (1+alpha*alpha)) for ReLU that are leaky with alpha
func GraphCollisionStats ¶
GraphCollisionStats returns the collisions in the graph only when built with the debug tag, otherwise it's a noop that returns 0
func HeEtAlN64 ¶
HeEtAlN64 returns float64 weights sampled from a normal distro, using the methods described in He et al (2015). The formula is:
randn(n) * sqrt(2/n)
See also https://arxiv.org/abs/1502.01852
For best results, use:
1.0 for gain for weights that will be used in linear and/or sigmoid units math.Sqrt(2.0) for gain for weights that will be used in ReLU units math.Sqrt(2.0 / (1+alpha*alpha)) for ReLU that are leaky with alpha
func HeEtAlU64 ¶
HeEtAlU64 returns float64 weights sampled from a uniform distro, using the methods described in He et al (2015). The formula is:
randn(n) * sqrt(2/n)
See also https://arxiv.org/abs/1502.01852
For best results, use:
1.0 for gain for weights that will be used in linear and/or sigmoid units math.Sqrt(2.0) for gain for weights that will be used in ReLU units math.Sqrt(2.0 / (1+alpha*alpha)) for ReLU that are leaky with alpha
func Let ¶
Let binds a Value to a node that is a variable. A variable is represented as a *Node with no Op. It is equivalent to :
x = 2
func Lift1Axial ¶
Lift1Axial; decorates a function with a precheck and post function lifting
func Lift2Broadcast ¶
func Lift2Broadcast(fn func(a, b *Node, pat1, pat2 []byte) (*Node, error)) func(a, b Input, pat1, pat2 []byte) Result
Lift2Broadcast decorates a function with a prechecl and post function lifting
func NewLispMachine ¶
NewLispMachine creates a VM that executes the graph as it is traversed. Depending on the VMOpts passed in this VM is also capable of performing automatic differentiation.
func NewTapeMachine ¶
NewTapeMachine creates a VM that compiles a graph into a prog.
func ReturnNode ¶
func ReturnNode(n *Node)
ReturnNode returns a node to the pool. It does not check that the *Node has been removed from the graph. USE WITH CAUTION.
func S ¶
S creates a tensor.Slice. end is optional. It should be passed in as the first param of the optionals. step is optional. It should be passed in as the second param of the optionals.
Default end is start+1. Default step is 1, unless end == step+1, then it defaults to 0
func SetDerivOf ¶
func SetDerivOf(deriv, of *Node)
SetDerivOf is used to hack around the fundamental limitations of Gorgonia.
Specifically it is used to set a node as the derivative of another node, used in the cuDNN version of batch norm.
The cuDNN BatchNorm operation produces the derivatives for the scale and bias as a side effect of calculating the derivative of the input. Because Gorgonia's Ops are modelled as pure functions (and no tuples) this causes a bit of trouble. With the clever use of scratch space ops multireturn can be simulated. But this causes derivatives to not be set correctly.
func SetOptimizationLevel ¶
func SetOptimizationLevel(i int)
SetOptimizationLevel sets the fast math optimization level. By default, fast math is turned off, and this function is a no-op.
Use the `fastmath` build tag to use fast math
func Uniform32 ¶
Uniform32 returns a []float64 drawn from a uniform distribution between [low, high) that is provided
func Uniform64 ¶
Uniform64 returns a []float64 drawn from a uniform distribution between [low, high) that is provided
func UnsafeLet ¶
UnsafeLet binds a Value to any node, not just a variable node. This means that you can use it to change any node's value at the runtime of the graph. UNSAFE!
Additional notes: if `be` is a tensor.Slice, and the node's op is a sliceOp or sliceIncrOp, the op's slice will be replaced with the new slice.
func Use ¶
func Use(b BLAS)
Use defines which BLAS implementation gorgonia should use. The default is Gonum's Native. These are the other options:
Use(blase.Implementation()) Use(cubone.Implementation()) Use(cgo.Implementation)
Note the differences in the brackets. The blase and cubone ones are functions.
func UseNonStable ¶
func UseNonStable()
UseNonStable turns off the stabilization functions when building graphs.
func UseStabilization ¶
func UseStabilization()
UseStabilization sets the global option to invoke stabilization functions when building the graph. Numerical stabilization is on by default
func ValueClose ¶
ValueClose checks whether two values are close to one another. It's predominantly used as an alternative equality test for floats
func WalkGraph ¶
WalkGraph walks a graph. It returns a channel of *Nodes, so be sure to consume the channel or there may be a deadlock
func WithGraphName ¶
func WithGraphName(name string) graphconopt
WithGraphName is a ExprGraph construction option that provides a name.
Types ¶
type ADOp ¶
type ADOp interface {
Op
DoDiff(ctx ExecutionContext, inputs Nodes, output *Node) error
}
An ADOp is an Op that supports automatic differentiation.
type AdaGradSolver ¶
type AdaGradSolver struct {
// contains filtered or unexported fields
}
AdaGradSolver is the solver that does adaptive gradient descent. Read the paper: http://jmlr.org/papers/v12/duchi11a.html
func NewAdaGradSolver ¶
func NewAdaGradSolver(opts ...SolverOpt) *AdaGradSolver
NewAdaGradSolver creates a new AdaGradSolver with sane-ish default values
func (*AdaGradSolver) Step ¶
func (s *AdaGradSolver) Step(model []ValueGrad) (err error)
Step steps through each node in the model and applies the Adaptive Gradient gradient descent algorithm on the value.
This function will error out if the nodes do not have an associated Grad value.
type AdamSolver ¶
type AdamSolver struct {
// contains filtered or unexported fields
}
AdamSolver is the Adaptive Moment Estimation solver (basically RMSProp on steroids). Paper: http://arxiv.org/abs/1412.6980
We overload the purpose of existing data structure of a *dualValue. However, instead of just holding a value and its derivative, the cache's *dualValues hold the Means of gradients (in .Value) and the variances of the gradients (in .d)
func NewAdamSolver ¶
func NewAdamSolver(opts ...SolverOpt) *AdamSolver
NewAdamSolver creates an Adam solver with these default values:
eta (learn rate) : 0.001 eps (smoothing factor) : 1e-8 beta1 : 0.9 beta2 : 0.999 batch : 1
func (*AdamSolver) Step ¶
func (s *AdamSolver) Step(model []ValueGrad) (err error)
Step steps through each node in the model and applies the Adaptive Moment Estimation gradient descent algorithm on the value.
This function will error out if the nodes do not have an associated Grad value.
type Arena ¶
type Arena interface {
Get(dev Device, size int64) (tensor.Memory, error) // Get returns a NoOpError when it cannot get a memory. Please allocate
GetFromValue(dev Device, v Value) (tensor.Memory, error) // Gets a memory and copies the values into the memory and returns it.
Put(dev Device, mem tensor.Memory, size int64) // puts the memory back into the arena
PutValue(dev Device, v Value) // puts the memory back into the arena
// Transfers memory from device to device
Transfer(toDev, fromDev Device, v Value, synchronous bool) (retVal Value, err error)
}
Arena is a representation of a pool of tensor.Memory
type AutoDiffError ¶
type AutoDiffError struct{}
AutoDiffError is an error which should be passed if the function is not differentiable. This is useful for Op implementations
func (AutoDiffError) Error ¶
func (err AutoDiffError) Error() string
type B ¶
type B bool
B represents a bool value.
func (*B) Data ¶
func (v *B) Data() interface{}
Data returns the original representation of the Value
func (*B) Pointer ¶
Pointer returns the pointer as an unsafe.Pointer. Satisfies the tensor.Memory interface
type BarzilaiBorweinSolver ¶
type BarzilaiBorweinSolver struct {
// contains filtered or unexported fields
}
BarzilaiBorweinSolver / Barzilai-Borwein performs Gradient Descent in steepest descend direction Solves 0 = F(x), by x_{i+1} = x_i - eta * Grad(F)(x_i) Where the learn rate eta is calculated by the Barzilai-Borwein method: eta(x_i) = <(x_i - x_{i-1}), (Grad(F)(x_i) - Grad(F)(x_{i-1}))> /
||(Grad(F)(x_i) - Grad(F)(x_{i-1}))||^2
The input learn rate is used for the first iteration. TODO: Check out stochastic implementations, e.g. "Barzilai-Borwein Step Size for Stochastic Gradient Descent" https://arxiv.org/abs/1605.04131
func NewBarzilaiBorweinSolver ¶
func NewBarzilaiBorweinSolver(opts ...SolverOpt) *BarzilaiBorweinSolver
NewBarzilaiBorweinSolver creates a new Barzilai-Borwein solver withs some default values: the learn rate is set to 0.001 and the solver does not use clipping.
func (*BarzilaiBorweinSolver) Step ¶
func (s *BarzilaiBorweinSolver) Step(model []ValueGrad) (err error)
Step steps through each node in the model and applies the Barzilai-Borwein gradient descent algorithm on the value.
This function will error out if the nodes do not have an associated Grad value.
type BatchNormOp ¶
type BatchNormOp struct {
// contains filtered or unexported fields
}
BatchNormOp is a batch normalization process as described by Ioffe and Szegedy (2015) - http://arxiv.org/abs/1502.03167
Normalization is done as:
γ(x - μ) / σ + β
γ is the scaling factor and β is the offset factor. These are created by BatchNorm()
func (*BatchNormOp) Do ¶
func (op *BatchNormOp) Do(values ...Value) (retVal Value, err error)
Do performs the batchnorm computation on the values
func (*BatchNormOp) DoDiff ¶
func (op *BatchNormOp) DoDiff(ctx ExecutionContext, inputs Nodes, output *Node) error
DoDiff does the gradient computation
func (*BatchNormOp) InferShape ¶
func (op *BatchNormOp) InferShape(ns ...DimSizer) (tensor.Shape, error)
InferShape from the input values
func (*BatchNormOp) OverwritesInput ¶
func (op *BatchNormOp) OverwritesInput() int
OverwritesInput is -1 (operator doesn't overwrite any input value)
func (*BatchNormOp) Reset ¶
func (op *BatchNormOp) Reset() error
Reset the operator by zeroing the internals scratch spaces
func (*BatchNormOp) SetTesting ¶
func (op *BatchNormOp) SetTesting()
SetTesting configure the op for testing mode
func (*BatchNormOp) SetTraining ¶
func (op *BatchNormOp) SetTraining()
SetTraining configure the op for training mode. A call to this function implicitly calls the Reset() method
func (*BatchNormOp) String ¶
func (op *BatchNormOp) String() string
func (*BatchNormOp) UsePreallocDo ¶
func (op *BatchNormOp) UsePreallocDo(prealloc Value, inputs ...Value) (retVal Value, err error)
UsePreallocDo ...
type Batched ¶
type Batched interface {
WorkAvailable() <-chan struct{}
DoWork()
}
Batched interface describes any object that can process batch work
type BatchedBLAS ¶
BatchedBLAS interface describes any object that can process BLAS work in batch
type BatchedDevice ¶
BatchedDevice is the superset of BatchedBLAS and the batched CUDA workflow.
type BroadcastPattern ¶
type BroadcastPattern byte
BroadcastPattern is actually a bit array. It's split into 2 nibbles - the left nibble represents the left operand, the right nibble represents the right operand:
xxxx|xxxx
The least significant bit of each nibble is elem 0. Concrete examples:
00000010 (0x02) = broadcast axis 1 of the right operand 00000001 (0x01) = broadcast axis 0 of the right operand 00000101 (0x09) = broadcast axis 0 AND axis 2 of the right operand 00010000 (0x10) = broadcast axis 0 of the left operand 00110000 (0x30) = broadcast axis 0 and axis 1 of the lef operand
You get the drill.
Do note that the current limitation of the BroadcastPattern allows only up to 4 dimensions per operand.
func NewBroadcastPattern ¶
func NewBroadcastPattern(leftAxes, rightAxes []byte) BroadcastPattern
NewBroadcastPattern is a helper function to create broadcast patterns
type CUDAADOp ¶
type CUDAADOp interface {
ADOp
CUDADoDiff(extern External, dev Device, inputs Nodes, output *Node) error
}
A CUDAADOp operation have a specific method to run with CUDA
type CUDADoer ¶
type CUDADoer interface {
CUDADo(extern External, dev Device, prealloc Value, inputs ...Value) (retVal Value, err error)
}
CUDADoer uses CUDA to perform the Op.
type CloneErrorer ¶
type CloneErrorer interface {
Clone() (interface{}, error)
}
CloneErrorer represents any type that can clone itself and return an error if necessary
type Cloner ¶
type Cloner interface {
Clone() interface{}
}
Cloner represents any type that can clone itself.
type CopierFrom ¶
type CopierFrom interface {
CopyFrom(src interface{}) error
}
CopierFrom represents any type that can copy data from the source provided.
type CopierTo ¶
type CopierTo interface {
CopyTo(dest interface{}) error
}
CopierTo represents any type that can copy data to the destination.
type Device ¶
type Device int
Device represents the device where the code will be executed on. In this build, all code will run on the CPU
const ( // CPU the only device the graph will be executed on CPU Device = 0 )
type DimSizer ¶
DimSizer is any type (typically a tensor.Shape) that allows querying for a dimension size given an input dimension.
func ShapesToDimSizers ¶
ShapesToDimSizers is a convenience function to convert a slice of tensor.Shape to a slice of DimSizer
type ExecutionContext ¶
ExecutionContext informs how an op should be executed
type ExprGraph ¶
type ExprGraph struct {
// contains filtered or unexported fields
}
ExprGraph is a data structure for a directed acyclic graph (of expressions). This structure is the main entry point for Gorgonia.
func (*ExprGraph) AddNode ¶
AddNode adds n to the graph. It panics if the added node ID matches an existing node ID.
func (*ExprGraph) AllNodes ¶
AllNodes is like Nodes, but returns Nodes instead of []graph.Node. Nodes() has been reserved for the graph.Directed interface, so this one is named AllNodes instead
func (*ExprGraph) ByName ¶
ByName returns nodes that have the name provided. Bear in mind that the name that is compared to is the internal name, not the result of calling node.Name(). The reason for doing this is for ease of finding only names that are user-supplied, instead of autogenerated names
func (*ExprGraph) Clone ¶
func (g *ExprGraph) Clone() interface{}
Clone clones the graph. All nodes gets cloned, and their values are cloned as well.
func (*ExprGraph) Constant ¶
Constant returns a constant that may be found in the graph. If no constant were found, a new one is created instead
func (*ExprGraph) Edge ¶
Edge returns the edge from u to v if such an edge exists and nil otherwise. The node v must be directly reachable from u as defined by the From method.
func (*ExprGraph) ExactSubgraphRoots ¶
ExactSubgraphRoots creates a subgraph from the roots provided. The difference between SubgraphRoots and ExactSubgraphRoots is that ExactSubGraphRoots will not attempt to discover if any nodes are missing.
Given a function like the following:
z = x + y set(x, -x.Grad) // setting the value of x to the negative of the gradient
When SubgraphRoots is used on z, the `-x.Grad` will be included. When using ExactSubgraphRoots, only `x` and `y` are included in the subgraph
func (*ExprGraph) HasEdgeBetween ¶
HasEdgeBetween returns whether an edge exists between nodes x and y without considering direction.
func (*ExprGraph) HasEdgeFromTo ¶
HasEdgeFromTo returns whether an edge exists in the graph from u to v.
func (*ExprGraph) Inputs ¶
Inputs returns a list of nodes which are inputs (that is to say, the user is required to set a value in it)
func (*ExprGraph) RemoveNode ¶
RemoveNode removes n from the graph, as well as any edges attached to it. If the node is not in the graph it is a no-op.
func (*ExprGraph) SetEdge ¶
SetEdge adds e, an edge from one node to another. If the nodes do not exist, they are added. It will panic if the IDs of the e.From and e.To are equal.
func (*ExprGraph) Subgraph ¶
Subgraph subsets a graph. This function has overloaded meanings - If only one node is passed in, it assumes that the one node is the root, otherwise, it treats ns as the subset of nodes to be included in the subgraph
func (*ExprGraph) SubgraphRoots ¶
SubgraphRoots creates a subgraph, assuming the provided nodes are roots to the new subgraph.
func (*ExprGraph) ToDot ¶
ToDot generates the graph in graphviz format. The use of this is to generate for the entire graph which may have multiple trees with different roots TODO: This is getting unwieldy. Perhaps refactor out into a ToDot(...Opt)?
func (*ExprGraph) UnbindAll ¶
func (g *ExprGraph) UnbindAll()
UnbindAll unbinds all the values from the nodes
func (*ExprGraph) UnbindAllNonInputs ¶
func (g *ExprGraph) UnbindAllNonInputs()
UnbindAllNonInputs unbinds all the values from nodes that aren't input nodes
type ExternMetadata ¶
ExternMetadata is used to hold metadata about external execution devices. In this build, it's an empty struct because the default build doesn't use external devices to execute the graph on
func (*ExternMetadata) Cleanup ¶
func (m *ExternMetadata) Cleanup()
Cleanup cleans up the ancillary allocations made during the calling of batched external device function.
The reason for this method is due to the fact that there is currently no way to free memory while the context is still running without causing some weirdness to the CUDA calls.
This is a No-op in this build
func (*ExternMetadata) DoWork ¶
func (m *ExternMetadata) DoWork() error
DoWork flushes any batched cgo calls. In this build it only flushes the batched BLAS calls.
func (*ExternMetadata) Get ¶
Get allocates a memory of the size. In this build it returns a NoOpError.
func (*ExternMetadata) GetFromValue ¶
GetFromValue allocates a memory of the size of v. In this build it returns a NoOpError, and v itself
func (ExternMetadata) HasFunc ¶
func (m ExternMetadata) HasFunc(name string) bool
HasFunc will always return false in this build
func (*ExternMetadata) Put ¶
func (m *ExternMetadata) Put(dev Device, mem tensor.Memory, size int64)
Put puts a previously allocated memory slab of the provided size back into the pool. Currently this is a No-op in this build.
func (*ExternMetadata) PutValue ¶
func (m *ExternMetadata) PutValue(dev Device, v Value)
PutValue puts a previously allocated value into the pool. In this build, it is a noop.
func (*ExternMetadata) Reset ¶
func (m *ExternMetadata) Reset()
Reset is a noop function for compatibility with the Cuda build
func (*ExternMetadata) Signal ¶
func (m *ExternMetadata) Signal()
Signal sends a signal down the workavailable channel, telling the VM to call the DoWork method. Signal is a synchronous method
func (*ExternMetadata) Sync ¶
func (m *ExternMetadata) Sync() chan struct{}
Sync returns the sync channel
func (*ExternMetadata) Transfer ¶
func (m *ExternMetadata) Transfer(toDev, fromDev Device, v Value, synchronous bool) (retVal Value, err error)
Transfer transfers a value from device to device. In this build, it's a noop, returning the input value, and a nil error
func (*ExternMetadata) WorkAvailable ¶
func (m *ExternMetadata) WorkAvailable() <-chan bool
WorkAvailable returns a channel of empty struct, which is used to signal to the VM when there is work available. The VM will then call the DoWork method.
type External ¶
type External interface {
Arena
Signal() // signals the machine to do work
Sync() chan struct{}
}
External is a representation of an external device (cuda/cgo/openCL), conceptually modelled as a machine.
type ExternalOp ¶
type ExternalOp struct {
Op
ExecutionContext
Prealloc Value
Incr Value // is this a Incr? IncrDoers have higher precedence over PreallocDo
UseUnsafe bool // Is this an unsafe op? Lowest of all "special" Dos
}
ExternalOp is an op that contains an external context. This allows for ops to be run without needing a VM
func NewAddOp ¶
func NewAddOp(a, b *Node, ctx ExecutionContext) *ExternalOp
NewAddOp creates a new *ExternalOp that wraps an add op
func NewExternalOp ¶
func NewExternalOp(op Op, ctx ExecutionContext, prealloc Value) *ExternalOp
NewExternalOp creates a new *ExternalOp.
func NewHadamardProdOp ¶
func NewHadamardProdOp(a, b *Node, ctx ExecutionContext) *ExternalOp
NewHadamardProdOp creates a new *ExternalOp that wraps a mul op
func NewSubOp ¶
func NewSubOp(a, b *Node, ctx ExecutionContext) *ExternalOp
NewSubOp creates a new *ExternalOp that wraps a sub op
func (*ExternalOp) DetermineDevice ¶
func (op *ExternalOp) DetermineDevice(inputs Nodes, output *Node) error
DetermineDevice ...
func (*ExternalOp) String ¶
func (op *ExternalOp) String() string
type F32 ¶
type F32 float32
F32 represents a float32 value.
func (*F32) Data ¶
func (v *F32) Data() interface{}
Data returns the original representation of the Value
func (*F32) Pointer ¶
Pointer returns the pointer as an unsafe.Pointer. Satisfies the tensor.Memory interface
type F64 ¶
type F64 float64
F64 represents a float64 value.
func (*F64) Data ¶
func (v *F64) Data() interface{}
Data returns the original representation of the Value
func (*F64) Pointer ¶
Pointer returns the pointer as an unsafe.Pointer. Satisfies the tensor.Memory interface
type I ¶
type I int
I represents a int value.
func (*I) Data ¶
func (v *I) Data() interface{}
Data returns the original representation of the Value
func (*I) Pointer ¶
Pointer returns the pointer as an unsafe.Pointer. Satisfies the tensor.Memory interface
type I32 ¶
type I32 int32
I32 represents a int32 value.
func (*I32) Data ¶
func (v *I32) Data() interface{}
Data returns the original representation of the Value
func (*I32) Pointer ¶
Pointer returns the pointer as an unsafe.Pointer. Satisfies the tensor.Memory interface
type I64 ¶
type I64 int64
I64 represents a int64 value.
func (*I64) Data ¶
func (v *I64) Data() interface{}
Data returns the original representation of the Value
func (*I64) Pointer ¶
Pointer returns the pointer as an unsafe.Pointer. Satisfies the tensor.Memory interface
type InitWFn ¶
InitWFn is a type of helper function to help initialize weights vector/matrices. It generates the backing required for the tensors.
It's typically used in closures
func Gaussian ¶
Gaussian creates a InitWFn with the specified parameters. Example Usage:
w := NewMatrix(g, Float64, WithName("w"), WithShape(2,2), WithInit(Gaussian(0, 1)))
This will create a backing slice of []float64, with the length of 4, and its values are drawn from a gaussian distro
func GlorotN ¶
GlorotN creates a InitWFn that populates a Value with weights normally sampled using Glorot et al.'s algorithm
func GlorotU ¶
GlorotU creates a InitWFn that populates a Value with weights uniformly sampled using Glorot et al.'s algorithm
func Ones ¶
func Ones() InitWFn
Ones creates an InitWfn that populates a Value with ones. See Zeroes() for more explanation.
func RangedFrom ¶
RangedFrom creates an InitWFn that populates a Value starting with the provided start, increamenting the number for each element in the value by 1
func Uniform ¶
Uniform creates a InitWFn with the specified parameters. Example Usage:
w := NewMatrix(g, Float64, WithName("w"), WithShape(2,2), WithInit(Uniform(-1, 1)))
This will create a backing slice of []float64, with the length of 4, and its values are drawn from a uniform distro
type Momentum ¶
type Momentum struct {
// contains filtered or unexported fields
}
Momentum is the stochastic gradient descent optimizer with momentum item.
func NewMomentum ¶
NewMomentum creates a new Momentum with sane-ish default values
type NoOpError ¶
type NoOpError interface {
NoOp() bool
}
NoOpError is an error returned when an operation does nothing.
type NoRetOp ¶
A NoRetOp is an Op that reads a value, but does not return any value. It's a representation of a not-pure function
type Node ¶
type Node struct {
// contains filtered or unexported fields
}
A Node is a node in the computation graph
func ApplyOpWithName ¶
ApplyOpWithName applies the op, and then gives the node the given name
func At ¶
At is a symbolic operation for getting a value at the provided coordinates. If the input is a scalar, all the coordinates MUST be 0, or else an error will be returned.
func BatchedMatMul ¶
BatchedMatMul returns a node representing the batched mat mul operation.
A list of transpose options are allowed. The
func BinaryXent ¶
BinaryXent is a convenience function for doing binary crossentropy stuff. The formula is as below:
-(y * logprob) + (1-y)(1-logprob)
func BinomialRandomNode ¶
BinomialRandomNode creates an input node that has a random op so that everytime the node is passed, random values will be plucked from a binomial distribution with the mean and stdev provided. The type of the node depends on the shape passed in. To get a scalar value at run time, don't pass in any shapes
Whilst technically the number of trials of a binomal distribution should be a discrete value (you can't have half a trial), to keep with API uniformity, trials is passed in as a float64, but will be truncated to an int at runtime.
func BroadcastAdd ¶
Add performs a add. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
Example ¶
By default, Gorgonia operations do not perform broadcasting. To do broadcasting, you would need to manually specify the operation
g := NewGraph()
a := NewVector(g, tensor.Float64, WithShape(2), WithName("a"), WithValue(tensor.New(tensor.WithBacking([]float64{100, 100}))))
b := NewMatrix(g, tensor.Float64, WithShape(2, 2), WithName("b"), WithValue(tensor.New(tensor.WithShape(2, 2), tensor.WithBacking([]float64{1, 1, 2, 2}))))
fmt.Printf("a = %v\nb =\n%v\n", a.Value(), b.Value())
_, err := Add(a, b)
fmt.Printf("a + b yields an error: %v\n\n", err)
// Note here the broadcasting of a is on the first axis, not the zeroth axis. Simply put, assume that it's already a (2,1) matrix.
ab, err := BroadcastAdd(a, b, []byte{1}, nil)
if err != nil {
fmt.Printf("uh oh, something went wrong: %v\n", err)
}
ba, err := BroadcastAdd(b, a, nil, []byte{1})
if err != nil {
fmt.Printf("uh oh, something went wrong: %v\n", err)
}
// Now, let's run the program
machine := NewTapeMachine(g)
defer machine.Close()
if err = machine.RunAll(); err != nil {
log.Fatal(err)
}
fmt.Printf("a +⃗ b =\n%v\n", ab.Value())
fmt.Printf("b +⃗ a =\n%v", ba.Value())
Output: a = [100 100] b = ⎡1 1⎤ ⎣2 2⎦ a + b yields an error: Failed to infer shape. Op: + false: Shape mismatch: (2) and (2, 2) a +⃗ b = ⎡101 101⎤ ⎣102 102⎦ b +⃗ a = ⎡101 101⎤ ⎣102 102⎦
func BroadcastEq ¶
Eq performs a eq. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
func BroadcastGt ¶
Gt performs a gt. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
func BroadcastGte ¶
Gte performs a gte. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
Example (CreatingTriangleMatrices) ¶
// Broadcasting is useful. We can create triangular dense matrices simply
g := NewGraph()
a := NewMatrix(g, tensor.Float64, WithShape(3, 1), WithName("a"), WithInit(RangedFrom(0)))
b := NewMatrix(g, tensor.Float64, WithShape(1, 4), WithName("b"), WithInit(RangedFrom(0)))
tl, err := BroadcastGte(a, b, true, []byte{1}, []byte{0})
if err != nil {
log.Fatalf("uh oh. Something went wrong %v", err)
}
tu, err := BroadcastLt(a, b, true, []byte{1}, []byte{0})
if err != nil {
log.Fatalf("uh oh. Something went wrong %v", err)
}
m := NewTapeMachine(g)
// PEDAGOGICAL:
// Uncomment the following code if you want to see what happens behind the scenes
// m.Close()
// logger := log.New(os.Stderr, "",0)
// m = NewTapeMachine(g, WithLogger(logger), WithWatchlist())
defer m.Close()
if err = m.RunAll(); err != nil {
log.Fatal(err)
}
fmt.Printf("triangular, lower:\n%v\n", tl.Value())
fmt.Printf("triangular, upper:\n%v\n", tu.Value())
Output: triangular, lower: ⎡1 0 0 0⎤ ⎢1 1 0 0⎥ ⎣1 1 1 0⎦ triangular, upper: ⎡0 1 1 1⎤ ⎢0 0 1 1⎥ ⎣0 0 0 1⎦
func BroadcastHadamardDiv ¶
HadamardDiv performs a hadamarddiv. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
func BroadcastHadamardProd ¶
HadamardProd performs a hadamardprod. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
func BroadcastLt ¶
Lt performs a lt. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
func BroadcastLte ¶
Lte performs a lte. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
func BroadcastNe ¶
Ne performs a ne. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
func BroadcastPow ¶
Pow performs a pow. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
func BroadcastSub ¶
Sub performs a sub. The operation is precomposed with a broadcast such that the shapes matches before operations commence.
func Concat ¶
Concat performs a concatenate on the provided axis and inputs.
Example ¶
g := NewGraph()
x := NewTensor(g, Float64, 4, WithShape(2, 3, 4, 5), WithInit(RangedFrom(0)), WithName("x"))
y := NewTensor(g, Float64, 4, WithShape(2, 3, 4, 5), WithInit(RangedFrom(120)), WithName("y"))
z, err := Concat(2, x, y)
if err != nil {
log.Fatal(err)
}
m := NewTapeMachine(g)
if err := m.RunAll(); err != nil {
log.Fatal(err)
}
tmp := fmt.Sprintf("z %v\n%v", z.Value().Shape(), z.Value())
fmt.Println(strings.Replace(tmp, "\n\n", "\n", -1)) // this is because
Output: z (2, 3, 8, 5) ⎡ 0 1 2 3 4⎤ ⎢ 5 6 7 8 9⎥ ⎢ 10 11 12 13 14⎥ ⎢ 15 16 17 18 19⎥ ⎢120 121 122 123 124⎥ ⎢125 126 127 128 129⎥ ⎢130 131 132 133 134⎥ ⎣135 136 137 138 139⎦ ⎡ 20 21 22 23 24⎤ ⎢ 25 26 27 28 29⎥ ⎢ 30 31 32 33 34⎥ ⎢ 35 36 37 38 39⎥ ⎢140 141 142 143 144⎥ ⎢145 146 147 148 149⎥ ⎢150 151 152 153 154⎥ ⎣155 156 157 158 159⎦ ⎡ 40 41 42 43 44⎤ ⎢ 45 46 47 48 49⎥ ⎢ 50 51 52 53 54⎥ ⎢ 55 56 57 58 59⎥ ⎢160 161 162 163 164⎥ ⎢165 166 167 168 169⎥ ⎢170 171 172 173 174⎥ ⎣175 176 177 178 179⎦ ⎡ 60 61 62 63 64⎤ ⎢ 65 66 67 68 69⎥ ⎢ 70 71 72 73 74⎥ ⎢ 75 76 77 78 79⎥ ⎢180 181 182 183 184⎥ ⎢185 186 187 188 189⎥ ⎢190 191 192 193 194⎥ ⎣195 196 197 198 199⎦ ⎡ 80 81 82 83 84⎤ ⎢ 85 86 87 88 89⎥ ⎢ 90 91 92 93 94⎥ ⎢ 95 96 97 98 99⎥ ⎢200 201 202 203 204⎥ ⎢205 206 207 208 209⎥ ⎢210 211 212 213 214⎥ ⎣215 216 217 218 219⎦ ⎡100 101 102 103 104⎤ ⎢105 106 107 108 109⎥ ⎢110 111 112 113 114⎥ ⎢115 116 117 118 119⎥ ⎢220 221 222 223 224⎥ ⎢225 226 227 228 229⎥ ⎢230 231 232 233 234⎥ ⎣235 236 237 238 239⎦
func Conv2d ¶
func Conv2d(im, filter *Node, kernelShape tensor.Shape, pad, stride, dilation []int) (retVal *Node, err error)
Conv2d is a simple 2D convoution, to be used for CPU computation only. If CuDNN is used, use the CUDAConv2D function. These are the properties the inputs must fulfil:
im: must have 4D shape. Expected format is BCHW (batch, channel, height, width) filter: must have 4D shape: (batch, kernel, height, width) kernelShape: shape of the filter kernel pad: len(pad) == 2 stride: len(stride) == 2 dilation: len(dilation) == 2
func Div ¶
Div is a shortcut function for HadamardDiv for scalar values. For matrix/tensor values, the matrix division operation is not yet handled, and will panic.
func Dropout ¶
Dropout is a convenience function to implement dropout. It uses randomly zeroes out a *Tensor with a probability drawn from a uniform distribution
func Eq ¶
Eq perfors a pointwise eq operation.
retSame indicates if the data type of the return value should be the same as the input data type. It defaults to Bool otherwise.
func GaussianRandomNode ¶
GaussianRandomNode creates an input node that has a random op so everytime the node is passed, random values will be plucked from a gaussian distribution with the mean and stdev provided. The type of the node depends on the shape passed in. To get a scalar value at run time, don't pass in any shapes
func GlobalAveragePool2D ¶
GlobalAveragePool2D consumes an input tensor X and applies average pooling across the values in the same channel. The expected input shape is BCHW where B is the batch size, C is the number of channels, and H and W are the height and the width of the data.
func Gt ¶
Gt perfors a pointwise gt operation.
retSame indicates if the data type of the return value should be the same as the input data type. It defaults to Bool otherwise.
func Gte ¶
Gte perfors a pointwise gte operation.
retSame indicates if the data type of the return value should be the same as the input data type. It defaults to Bool otherwise.
func HadamardDiv ¶
HadamardDiv perfors a pointwise hadamarddiv operation.
func HadamardProd ¶
HadamardProd perfors a pointwise hadamardprod operation.
func Im2Col ¶
Im2Col converts a BCHW image block to columns. The kernel, pad and stride parameter must be shape of size 2, no more no less This poor naming scheme clearly comes from matlab
func InverseSqrt ¶
InverseSqrt performs a pointwise inversesqrt.
func KeepDims ¶
KeepDims is a function that ensures that input and output dimensions are the same though the shape may change.
The expandLeft flag in the function indicates if any shape expansion should be done leftwards or rightwards. For example, if fn() returns a tensor with a shape (3) and the desired dimension is 2, then if `expandLeft` is true the result will be `(1, 3)`. Otherwise the result will be `(3, 1)`.
At the moment, results that turn into scalars cannot have their dimensions kept - the semantics isn't well established yet and is a work in progress.
func LeakyRelu ¶
LeakyRelu returns a node whose underlying value is:
f(x) = alpha * x if x < 0 f(x) = x for x >= 0
applied elementwise.
func Lt ¶
Lt perfors a pointwise lt operation.
retSame indicates if the data type of the return value should be the same as the input data type. It defaults to Bool otherwise.
func Lte ¶
Lte perfors a pointwise lte operation.
retSame indicates if the data type of the return value should be the same as the input data type. It defaults to Bool otherwise.
func MaxPool2D ¶
MaxPool2D applies the kernel filter to the input node. The pad slice can have two different lengths.
- if len(pad) == 2, padding is assume to be symetric, and a padding is adding up *and* down to each dimension paddedOutputH = pad[0] + inputH + pad[0] paddedOutputW = pad[1] + inputW + pad[1]
- if len(pad) == 4, padding is explicit and can be asymmetric. paddedOutputH = pad[0] + inputH + pad[1] paddedOutputW = pad[2] + inputW + pad[3]
func Mul ¶
Mul is the general handler for multiplication of nodes. It is extremely overloaded. Only use if you know what you're doing
If any of the nodes are ScalarType, then it'll be redirected to HadamardProd() instead If the nodes are both vectors (that is, have a shape of (x, 1) or (1, x)), then the operator used will be a vectorDot If only one of the nodes is a vector, then the operator used will be a matrix-vector multiplication will be used, and most importantly, a transpose will be used (when necessary) If both nodes are matrices, then well, matrix multiplication will be done
func Must ¶
func Must(n *Node, err error, opts ...NodeConsOpt) *Node
Must indicates a node must be created. If there isn't a node created, or there was an error, it subsumes the error, and immediately panics
func Ne ¶
Ne perfors a pointwise ne operation.
retSame indicates if the data type of the return value should be the same as the input data type. It defaults to Bool otherwise.
func NegNegOptimization ¶
NegNegOptimization optimizes away -(-x) to just return x place before neg
func NewConstant ¶
func NewConstant(v interface{}, opts ...NodeConsOpt) *Node
NewConstant takes in any reasonable value and makes it a constant node.
func NewMatrix ¶
func NewMatrix(g *ExprGraph, t tensor.Dtype, opts ...NodeConsOpt) *Node
NewMatrix creates a Node representing a variable that holds a matrix (nxm)
func NewScalar ¶
func NewScalar(g *ExprGraph, t tensor.Dtype, opts ...NodeConsOpt) *Node
NewScalar creates a Node representing a variable that holds a scalar value
func NewTensor ¶
NewTensor creates a Node representing a variable that holds a tensor (any n-dimensional array with dimensions greater than 2)
func NewUniqueNode ¶
func NewUniqueNode(opts ...NodeConsOpt) *Node
NewUniqueNode creates a new unique node in a graph. If no graph was specified in the construction options then it will just return a graphless node.
func NewVector ¶
func NewVector(g *ExprGraph, t tensor.Dtype, opts ...NodeConsOpt) *Node
NewVector creates a Node representing a variable that holds a vector (nx1 matrix)
func NodeFromAny ¶
func NodeFromAny(g *ExprGraph, any interface{}, opts ...NodeConsOpt) *Node
NodeFromAny creates a Node from a tensor.Tensor, automatically filling in shape and type info
func Norm ¶
Norm returns the p-norm of a Value. Use p=2 if you want to use unordered norms.
This is a simpler version of the norms found in the Tensor package, which specializes and optimizes even more (well, given it's adapted from Numpy, it is clearly way more optimized)
func OneHotVector ¶
func OneHotVector(id, classes int, t tensor.Dtype, opts ...NodeConsOpt) *Node
OneHotVector creates a node representing a one hot vector
func OuterProd ¶
OuterProd returns a Node representing the outer product of two vectors. This function will return an error if both input nodes are not vectors
func Read ¶
Read is one of those special snowflake tumblrina *Nodes. It allows for extraction of the value of the *Node at runtime into a Value. Note that a *Value (a pointer to a Value) is passed into this function, not a Value.
func Rectify ¶
Rectify is a convenience function for creating rectified linear units activation functions. This function uses >=, which is the canonical version. If you want to use >, you can create your own by just following this.
func ReduceAdd ¶
func ReduceAdd(nodes Nodes, opts ...NodeConsOpt) (retVal *Node, err error)
ReduceAdd takes a slice of *Nodes, and folds them into one by adding
func ReduceMul ¶
func ReduceMul(nodes Nodes, opts ...NodeConsOpt) (retVal *Node, err error)
ReduceMul is like foldl(*, nodes)
func Slice ¶
Slice slices a *Node. For T[:] slices, pass in nil. Will error out if node's type is not a Tensor
func SoftMax ¶
SoftMax performs softmax on the input. Specifically this is used:
e^(a[i]) / sum((e^(a[i])))
For a more numerically stable SoftMax, use StableSoftMax. TODO: MULTI RANK SOFTMAX
Example ¶
g := NewGraph()
t := tensor.New(tensor.WithShape(2, 3), tensor.WithBacking([]float64{1, 3, 2, 3, 2, 1}))
u := t.Clone().(*tensor.Dense)
v := tensor.New(tensor.WithShape(2, 2, 3), tensor.WithBacking([]float64{
1, 3, 2,
4, 2, 1,
3, 5, 3,
2, 1, 5,
}))
a := NodeFromAny(g, t, WithName("a"))
b := NodeFromAny(g, u, WithName("b"))
c := NodeFromAny(g, v, WithName("c"))
sm1 := Must(SoftMax(a))
sm0 := Must(SoftMax(b, 0))
sm := Must(SoftMax(c))
m := NewTapeMachine(g)
if err := m.RunAll(); err != nil {
log.Fatal(err)
}
fmt.Printf("a:\n%v\nsoftmax(a) - along last axis (default behaviour):\n%1.2f", a.Value(), sm1.Value())
fmt.Printf("b:\n%v\nsoftmax(b) - along axis 0:\n%1.2f", b.Value(), sm0.Value())
tmp := fmt.Sprintf("c %v:\n%v\nsoftmax(c) - along last axis (default behaviour) %v:\n%1.2f", c.Value().Shape(), c.Value(), sm.Value().Shape(), sm.Value())
fmt.Println(strings.Replace(tmp, "\n\n\n", "\n\n", -1))
// the requirement to use tmp and strings.Replace is because when Go runs example tests, it strips excess newlines.
Output: a: ⎡1 3 2⎤ ⎣3 2 1⎦ softmax(a) - along last axis (default behaviour): ⎡0.09 0.67 0.24⎤ ⎣0.67 0.24 0.09⎦ b: ⎡1 3 2⎤ ⎣3 2 1⎦ softmax(b) - along axis 0: ⎡0.12 0.73 0.73⎤ ⎣0.88 0.27 0.27⎦ c (2, 2, 3): ⎡1 3 2⎤ ⎣4 2 1⎦ ⎡3 5 3⎤ ⎣2 1 5⎦ softmax(c) - along last axis (default behaviour) (2, 2, 3): ⎡0.09 0.67 0.24⎤ ⎣0.84 0.11 0.04⎦ ⎡0.11 0.79 0.11⎤ ⎣0.05 0.02 0.94⎦
func StableSoftMax ¶
StableSoftMax performs a numerically stable softmax on the input. Specifically this is the formula used:
e^(a - max(a)) / sum(e^(a - max(a)))
func UniformRandomNode ¶
UniformRandomNode creates an input node that has a random op so everytime the node is passed, random values will be plucked from a uniform distribution. The type of the node depends on the shape passed in. To get a scalar value at run time, don't pass in any shapes
func (*Node) Clone ¶
func (n *Node) Clone() (retVal interface{})
Clone clones the node. There are some caveats:
- the graph is not copied over - the node essentially does not belong to a collection
- there is no ID
- the children are not cloned
func (*Node) CloneTo ¶
CloneTo clones the node into a new graph. If CloneTo() is called on the same graph as the n, it will return n. The reason this is done is because at any given time, every node should be unique in the *ExprGraph.
TODO: clone children as well (this means that CloneTo() is only currently suitable fo input nodes)
func (*Node) Err ¶
Err always returns nil. However, this method is implemented to enable nicer composition of functions
func (*Node) GradOnDevice ¶
func (n *Node) GradOnDevice(dev Device, extern External) (retVal Value, allocOnExtern bool, err error)
GradOnDevice gets the gradient value of the node as a Value but on the desired device. In this build the device is always CPU, so it's equivalent to calling .Grad()
func (*Node) Hashcode ¶
Hashcode provides the hash for the tree, assuming that the node is the root of the tree. Original implementation was here by Vatine (who's apparently 80 years old and using SO!?!):
http://stackoverflow.com/questions/1988665/hashing-a-tree-structure
func (*Node) IsColVec ¶
IsColVec indicates if a node represents a Column Vector. This is based on the type of the node, not the actual value associated with the node
func (*Node) IsMatrix ¶
IsMatrix indicates if a node represents a matrix. This is based on the type of the node, not the actual value associated with the node
func (*Node) IsRowVec ¶
IsRowVec indicates if a node represents a Row Vector. This is based on the type of the node, not the actual value associated with the node
func (*Node) IsScalar ¶
IsScalar indicates if a node represents a a scalar value. This is based on the type of the node, not the actual value associated with the node
func (*Node) IsVar ¶
IsVar returns true if the node represents a differentiable variable (i.e. it's an argument to the function that is not a statement)
func (*Node) IsVector ¶
IsVector indicates if a node represents a vector value. This is based on the type of the node, not the actual value associated with the node
func (*Node) Name ¶
Name returns the name of the node. If a name was specified and it is too long, the short name will be used instead (except in inputs)
The short name is typically of the form: OpName(%1, %2 ...), making it read more like a function call
func (*Node) Node ¶
Node returns itself. This sorts of monoidal patterns are useful for compositions via interfaces.
func (*Node) Nodes ¶
Nodes returns n as a slice of *Node. Again, this is mostly useful for interfaces
func (*Node) RestrictedToDot ¶
RestrictedToDot prints the graphviz compatible string but does not print the entire tree up and down indicates how many levels to look up, and how many levels to look down
func (*Node) ToDot ¶
ToDot returns the graph as a graphviz compatible string. DEPRECATED: This function will be removed in the next release, please use the encoding/dot package
type NodeConsOpt ¶
type NodeConsOpt func(*Node)
NodeConsOpt is a function that provides construction options for any Node.
func In ¶
func In(g *ExprGraph) NodeConsOpt
In is a node construction option to set a node's graph. A `*Node`'s graph is immutable. If the graph has already been set, a check will be made that the specifiec *Graph and the *Graph set in *Node are the same. If they are not, the function will panic/
func WithChildren ¶
func WithChildren(children Nodes) NodeConsOpt
WithChildren sets the children of a node to the specified chidren. This construction option does NOT check if existing children exists, and will overwrite the existing children.
func WithGrad ¶
func WithGrad(any interface{}) NodeConsOpt
WithGrad is a node construction option that binds the value to the *Node. This function may panic if:
- There isn't already a value associated with the node (.boundTo == nil)
- The type of the Value does not match the value of the node.
func WithGroupName ¶
func WithGroupName(name string) NodeConsOpt
WithGroupName is a node construction option to group a *Node within a particular group. This option is useful for debugging with graphs. This function is deprecated and will proabably be remove in the next version.
func WithInit ¶
func WithInit(fn InitWFn) NodeConsOpt
WithInit is a node construction option to initialize a *Node with the InitWFn provided.
func WithName ¶
func WithName(name string) NodeConsOpt
WithName is a node construction option that gives the *Node the provided name. This is especially useful in debugging graphs.
func WithOp ¶
func WithOp(op Op) NodeConsOpt
WithOp is a node construction option to set a node's Op to the specified Op. `Op`s in `*Node`s are immutable once set and cannot be changed. If the node already has an Op specified a check will be made to see if the provided Op and the one already specified in the `*Node` is the same - do note that comparison of Ops is done using the `Hashcode()` method of Ops, and hash collisions MAY occur - If both ops are different, this function will panic.
func WithShape ¶
func WithShape(shp ...int) NodeConsOpt
WithShape is a node construction option to initialize a *Node with a particular shape. This function panics if the shape's dimensions do not match the specified dimensions of the *Node.
func WithType ¶
func WithType(t hm.Type) NodeConsOpt
WithType is a node construction option to set a node to the specified type. Types in *Node are immutable once set. If the type has already been specified in the node, a check will be made to see if the both types are the same. If it isn't, it will panic.
func WithValue ¶
func WithValue(any interface{}) NodeConsOpt
WithValue is a node construction option that binds the value to the *Node. This function may panic if:
- Gorgonia was unable to convert interface{} into a Value.
- The type of the Value does not match the type of the nodes.
type NodeSet ¶
type NodeSet map[*Node]struct{}
NodeSet is the primary type that represents a set
func NewNodeSet ¶
NewNodeSet creates and returns a reference to an empty set.
func (NodeSet) Cardinality ¶
Cardinality returns how many items are currently in the set.
func (*NodeSet) Clear ¶
func (set *NodeSet) Clear()
Clear clears the entire set to be the empty set.
func (NodeSet) ContainsAll ¶
ContainsAll determines if the given items are all in the set
func (NodeSet) Difference ¶
Difference returns a new set with items in the current set but not in the other set
func (NodeSet) Equal ¶
Equal determines if two sets are equal to each other. If they both are the same size and have the same items they are considered equal. Order of items is not relevant for sets to be equal.
func (NodeSet) IsSuperset ¶
IsSuperset determines if every item of this set is in the other set.
func (NodeSet) SymmetricDifference ¶
SymmetricDifference returns a new set with items in the current set or the other set but not in both.
type Nodes ¶
type Nodes []*Node
Nodes is a slice of nodes, but it also acts as a set of nodes by implementing the Sort interface
func Backpropagate ¶
Backpropagate backpropagates errors by performing revers-emode symbolic differentiation, starting from the outputs, and working its way towads the inputs.
This is the rough algorithm:
- Filter out nodes that are unreachable
- Forwards analysis, where a list of nodes affecting the output is added to consideration
- Backwards analysis, where a list of nodes affected by differentiating the output are added to the consideration
- If there is a difference in both sets, it will cause an error (both sets should be the same)
- Traverse the graph from output towards input. On each visit, perform the symbolic differentiation
For most cases, Grad() should be used instead of Backpropagate(), as Grad() performs several checks which would be the general use case, before calling Backpropagate()
func NodesFromInputs ¶
NodesFromInputs creates a Nodes from a list of Input.
func Sort ¶
Sort topologically sorts a ExprGraph: root of graph will be first nodes are sorted using gonum's SortStabilized function.
see https://godoc.org/gonum.org/v1/gonum/graph/topo#SortStabilized for more info
func Unconcat ¶
Unconcat is the opposite of the built in concat function TODO: port this back to Gorgonia and use Gorgonia's sli instead
Example ¶
g := NewGraph()
x := NewTensor(g, Float64, 4, WithShape(2, 3, 4, 5), WithInit(RangedFrom(0)), WithName("x"))
y := NewTensor(g, Float64, 4, WithShape(2, 3, 4, 5), WithInit(RangedFrom(120)), WithName("y"))
z, err := Concat(2, x, y)
if err != nil {
log.Fatal(err)
}
unconcats, err := Unconcat(z, 2, 2)
if err != nil {
log.Fatal(err)
}
a, b := unconcats[0], unconcats[1]
m := NewTapeMachine(g)
if err := m.RunAll(); err != nil {
log.Fatal(err)
}
tmp := fmt.Sprintf("a %v\n%v\nb %v\n%v", a.Value().Shape(), a.Value(), b.Value().Shape(), b.Value())
fmt.Println(strings.Replace(tmp, "\n\n", "\n", -1))
Output: a (2, 3, 4, 5) ⎡ 0 1 2 3 4⎤ ⎢ 5 6 7 8 9⎥ ⎢ 10 11 12 13 14⎥ ⎣ 15 16 17 18 19⎦ ⎡ 20 21 22 23 24⎤ ⎢ 25 26 27 28 29⎥ ⎢ 30 31 32 33 34⎥ ⎣ 35 36 37 38 39⎦ ⎡ 40 41 42 43 44⎤ ⎢ 45 46 47 48 49⎥ ⎢ 50 51 52 53 54⎥ ⎣ 55 56 57 58 59⎦ ⎡ 60 61 62 63 64⎤ ⎢ 65 66 67 68 69⎥ ⎢ 70 71 72 73 74⎥ ⎣ 75 76 77 78 79⎦ ⎡ 80 81 82 83 84⎤ ⎢ 85 86 87 88 89⎥ ⎢ 90 91 92 93 94⎥ ⎣ 95 96 97 98 99⎦ ⎡100 101 102 103 104⎤ ⎢105 106 107 108 109⎥ ⎢110 111 112 113 114⎥ ⎣115 116 117 118 119⎦ b (2, 3, 4, 5) ⎡120 121 122 123 124⎤ ⎢125 126 127 128 129⎥ ⎢130 131 132 133 134⎥ ⎣135 136 137 138 139⎦ ⎡140 141 142 143 144⎤ ⎢145 146 147 148 149⎥ ⎢150 151 152 153 154⎥ ⎣155 156 157 158 159⎦ ⎡160 161 162 163 164⎤ ⎢165 166 167 168 169⎥ ⎢170 171 172 173 174⎥ ⎣175 176 177 178 179⎦ ⎡180 181 182 183 184⎤ ⎢185 186 187 188 189⎥ ⎢190 191 192 193 194⎥ ⎣195 196 197 198 199⎦ ⎡200 201 202 203 204⎤ ⎢205 206 207 208 209⎥ ⎢210 211 212 213 214⎥ ⎣215 216 217 218 219⎦ ⎡220 221 222 223 224⎤ ⎢225 226 227 228 229⎥ ⎢230 231 232 233 234⎥ ⎣235 236 237 238 239⎦
func UnstableSort ¶
UnstableSort performs a topological sort of the directed graph g returning the 'from' to 'to' sort order. If a topological ordering is not possible, an Unorderable error is returned listing cyclic components in g with each cyclic component's members sorted by ID. When an Unorderable error is returned, each cyclic component's topological position within the sorted nodes is marked with a nil graph.Node.
func (Nodes) AllSameGraph ¶
AllSameGraph returns true if all the nodes in the slice belong to the same graph. Note that constants do not have to belong to the same graph.
func (Nodes) Difference ¶
Difference is ns - other. Bear in mind it is NOT commutative
func (Nodes) Format ¶
Format implements fmt.Formatter, which allows Nodes to be differently formatted depending on the verbs
func (Nodes) Node ¶
Node returns nil. Always. This is bound to cause a panic somewhere if an program is not using it correctly. The reason for implementing this is so that it may fulfil common interfaces.
type Op ¶
type Op interface {
// Arity returns the number of inputs the Op expects. -1 indicates that it's n-ary and will be determined at runtime
Arity() int
// Informs the type of the Op (not the node). This will be used by the type system to infer the final type of the node
Type() hm.Type
// returns the output shape as a function of the inputs
InferShape(...DimSizer) (tensor.Shape, error)
// executes the op
Do(...Value) (Value, error)
// indicates if the Op will return a pointer (allowing possible inplace edits) or by value
// if it's false, the return value of the Op will be a copy of its input
ReturnsPtr() bool
// Does this op potentially call external (cgo or cuda) functions (thereby requiring extra overhead for Go's trampolining thing)
CallsExtern() bool
// overwriteInput() is a method which states which input the output will be overwriting.
// This allows for some efficiency gains as the underlying arrays wouldn't have to be re-allocated.
// The method returns an int instead of a bool because potentially different operations may be allowed
// to overwrite certain inputs. For example, consider an operation to increment a value:
// the IncrementOp would be a unary operator, and assuming we would like to overwrite the input,
// the retVal of overwriteInput() will be 0 (inputs[0]).
// -1 is returned if overwriting of input is disallowed
OverwritesInput() int
/* Other methods */
WriteHash(h hash.Hash)
Hashcode() uint32
fmt.Stringer
}
An Op is a symbolic representation of an operation Think of them as functions, taking an input (or multiple), and outputting something
All Ops have type signatures that look like this:
OpName :: (Floats a) ⇒ Tensor a → Tensor a → Tensor a
type RMSPropSolver ¶
type RMSPropSolver struct {
// contains filtered or unexported fields
}
RMSPropSolver is a solver that implements Geoffrey Hinton's RMSProp gradient descent optimization algorithm. http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
func NewRMSPropSolver ¶
func NewRMSPropSolver(opts ...SolverOpt) *RMSPropSolver
NewRMSPropSolver creates an RMSProp solver with these default values:
eta (learn rate) : 0.001 eps (smoothing factor): 1e-8 rho (decay factor) : 0.999
func (*RMSPropSolver) Step ¶
func (s *RMSPropSolver) Step(model []ValueGrad) (err error)
Step steps through each node in the model and applies the RMSProp gradient descent algorithm on the value.
This function will error out if the nodes do not have an associated Grad value.
type ReductionOp ¶
ReductionOp changes the shape of the node
type Result ¶
Result is either a Node or Nodes or error. It's a poor man's sum types and it's not sealed for good reason
func LiftResult ¶
type SDOp ¶
type SDOp interface {
Op
// DiffWRT indicates if the op is differentiable with regards to the given number of inputs
// returns []bool to indicate which input it is differentiable to
DiffWRT(inputs int) []bool
// SymDiff symbolically differentiates the op
SymDiff(inputs Nodes, output, grad *Node) (retVal Nodes, err error)
}
A SDOp is an Op that supports symbolic differentiation
type Scalar ¶
type Scalar interface {
Value
// contains filtered or unexported methods
}
Scalar represents a scalar(non-array-based) value. Do note that it's the pointers of the scalar types (F64, F32, etc) that implement the Scalar interface. The main reason is primarily due to optimizations with regards to memory allocation and copying for device interoperability.
type Solver ¶
Solver is anything that does gradient updates. The name solvers is stolen from Caffe. A much shorter name than GradientUpdaters
type SolverOpt ¶
type SolverOpt func(s Solver)
SolverOpt is a function that provides construction options for a Solver
func WithBatchSize ¶
WithBatchSize sets the batch size for the solver. Currently only Adam and Vanilla (basic SGD) has batch size support
func WithClip ¶
WithClip clips the gradient if it gets too crazy. By default all solvers do not have any clips attached
func WithL1Reg ¶
WithL1Reg adds a L1 regularization parameter to the solver. By default, the solvers do not use any regularization param
func WithL2Reg ¶
WithL2Reg adds a L2 regularization parameter to the solver. By default, the solvers do not use any regularization param
func WithLearnRate ¶
WithLearnRate sets the learn rate or step size for the solver.
func WithMomentum ¶
WithMomentum sets the momentum of the solver. It is a no-op is the solver's type is not Momentum
type StandardEngine ¶
StandardEngine is the default CPU engine for gorgonia
type SymDiffError ¶
type SymDiffError struct {
// contains filtered or unexported fields
}
SymDiffError provides the context at which an error occurred
func (SymDiffError) Error ¶
func (err SymDiffError) Error() string
func (SymDiffError) Grad ¶
func (err SymDiffError) Grad() *Node
Grad returns a specific grad involved in the error
func (SymDiffError) Grads ¶
func (err SymDiffError) Grads() map[*Node]Nodes
Grads returns the grads involved in the error
func (SymDiffError) Node ¶
func (err SymDiffError) Node() *Node
Node returns a specific node involved in the error
func (SymDiffError) Nodes ¶
func (err SymDiffError) Nodes() Nodes
Nodes returns the nodes involved in the error
type Tensor ¶
type Tensor interface {
// info about the ndarrayN
Shape() tensor.Shape
Strides() []int
Dtype() tensor.Dtype
Dims() int
Size() int
DataSize() int
// type overloading methods
IsScalar() bool
ScalarValue() interface{}
// engine/memory related stuff
// all Tensors should be able to be expressed of as a slab of memory
// Note: the size of each element can be acquired by T.Dtype().Size()
Engine() tensor.Engine // Engine can be nil
MemSize() uintptr // the size in memory
Uintptr() uintptr // the pointer to the first element, as a uintptr
Pointer() unsafe.Pointer // the pointer to the first elemment as a unsafe.Ponter
IsNativelyAccessible() bool // Can Go access the memory
IsManuallyManaged() bool // Must Go manage the memory
}
Tensor is an interface that describes an ndarray
type TensorType ¶
TensorType is a type constructor for tensors.
Think of it as something like this:
data Tensor a = Tensor d a
The shape of the Tensor is not part of TensorType. Shape checking is relegated to the dynamic part of the program run
func (TensorType) Apply ¶
func (t TensorType) Apply(sub hm.Subs) hm.Substitutable
Apply applies the substitutions on the types. Satisfies the hm.Type interface.
func (TensorType) Eq ¶
func (t TensorType) Eq(other hm.Type) bool
Eq is the equality function of this type. The type of Tensor has to be the same, and for now, only the dimensions are compared. Shape may be compared in the future for tighter type inference. Satisfies the hm.Type interface.
func (TensorType) Format ¶
func (t TensorType) Format(state fmt.State, c rune)
Format implements fmt.Formatter. It is also required for the satisfication the hm.Type interface.
func (TensorType) FreeTypeVar ¶
func (t TensorType) FreeTypeVar() hm.TypeVarSet
FreeTypeVar returns any free (unbound) type variables in this type. Satisfies the hm.Type interface.
func (TensorType) Name ¶
func (t TensorType) Name() string
Name returns the name of the type, which will always be "Tensor". Satisfies the hm.Type interface.
func (TensorType) Normalize ¶
func (t TensorType) Normalize(k, v hm.TypeVarSet) (hm.Type, error)
Normalize normalizes the type variable names (if any) in the TensorType. Satisfies the hm.Type interface.
func (TensorType) String ¶
func (t TensorType) String() string
String implements fmt.Stringer and runtime.Stringer. Satisfies the hm.Type interface.
func (TensorType) Types ¶
func (t TensorType) Types() hm.Types
Types returns a list of types that TensorType contains - in this case, the type of Tensor (float64, float32, etc). Satisfies the hm.Type interface.
type U8 ¶
type U8 byte
U8 represents a byte value.
func (*U8) Data ¶
func (v *U8) Data() interface{}
Data returns the original representation of the Value
func (*U8) Pointer ¶
Pointer returns the pointer as an unsafe.Pointer. Satisfies the tensor.Memory interface
type UnsafeDoer ¶
UnsafeDoer is an op that will overwrite the underlying value.
type UsePreallocDoer ¶
UsePreallocDoer is an op that works when a preallocated value is provided
type VM ¶
type VM interface {
RunAll() error
Reset()
// Close closes all the machine resources (CUDA, if any, loggers if any)
Close() error
}
VM represents a structure that can execute a graph or program. There are two VMs (both unexported):
- *tapeMachine
- *lispMachine
The *tapeMachine pre-compiles a graph into a list of instructions, then executes the instructions linearly and sequentially. The main tradeoff is dynamism. Graphs cannot be dynamically created on the fly as a re-compilation process is required (and compilation is relatively expensive). However, graphs executed with the *tapeMachine run much faster as plenty of optimizations has been done in the code generation stage.
The *lispMachine allows for graphs to be dynamically built and executed upon. The tradeoff is that executing a graph on *lispMachine is generally slower than on *tapeMachine, given the same static "image" of a graph.
type VMOpt ¶
type VMOpt func(m VM)
VMOpt is a VM creation option
func BindDualValues ¶
BindDualValues is an option for *tapeMachine only. This is useful to set when using a Solver
func ExecuteBwdOnly ¶
func ExecuteBwdOnly() VMOpt
ExecuteBwdOnly creates a VM that will execute a graph by doing back propagation only. The assumption is of course, that the forward graph has already been executed, and there are already values associated with the nodes. This option is only for *lispMachine. Try it on any other VMs and it will panic.
func ExecuteFwdOnly ¶
func ExecuteFwdOnly() VMOpt
ExecuteFwdOnly creates a VM that will execute a graph forwards only - it will not do back propagation. This option is only for *lispMachine. Try it on any other VMs and it will panic.
func LogBothDir ¶
func LogBothDir() VMOpt
LogBothDir logs both directions of the execution of the graph. This option is only available for *lispMachine.
func LogBwd ¶
func LogBwd() VMOpt
LogBwd logs the backwards execution of a graph. This option is only for *lispMachine. Try it on any other VMs and it will panic.
func LogFwd ¶
func LogFwd() VMOpt
LogFwd logs the forward execution of a graph. This option is only for *lispMachine. Try it on any other VMs and it will panic.
func TraceExec ¶
func TraceExec() VMOpt
TraceExec is an option for *tapeMachine only. It stores an immutable copy of the executed value into the node, instead of a mutable value, which may be clobbered
func UseCudaFor ¶
UseCudaFor is an option for *tapeMachine. This function is NO-OP unless the program is built with the `cuda` tag.
func WithEngine ¶
WithEngine sets the tensor engine for computation inside the VM.
func WithInfWatch ¶
func WithInfWatch() VMOpt
WithInfWatch creates a VM that will watch for Infs when executing. It watches for +Inf, -Inf and Inf. No choice there. This slows the execution down.
func WithLogger ¶
WithLogger creates a VM with the supplied logger. If the logger is nil, a default logger, writing to os.stderr will be created.
func WithManualGradient ¶
func WithManualGradient() VMOpt
WithManualGradient allows the user to set the gradient of the root, before backprop. The root gradients should be set using the SetDeriv method
func WithNaNWatch ¶
func WithNaNWatch() VMOpt
WithNaNWatch creates a VM that will watch for NaNs when executing. This slows the execution down.
func WithPrecompiled ¶
WithPrecompiled is an option to pass in compiled programs. This is useful for users who use the CompileFunction function
func WithValueFmt ¶
WithValueFmt defines how the logger will output the values. It defaults to "%3.3f"
func WithWatchlist ¶
func WithWatchlist(list ...interface{}) VMOpt
WithWatchlist creates a VM with a watchlist. When the execution touches the things in the watchlist, the VM's logger will the log it. This allows for watching and finetuning of the algorithm. When nothing is passed in, then the VM will default to watching and logging every single execution object.
The watchlist allows for different things to be watched, depending on VM type:
*lispMachine will ONLY take *Node *tapeMachine will take int (for register IDs) or *Node.
type Value ¶
type Value interface {
Shape() tensor.Shape // Shape returns the shape of the Value. Scalar values return ScalarShape()
Size() int // Size represents the number of elements in the Value. Note that in cases such as a *tensor.Dense, the underlying slice MAY have more elements than the Size() reports. This is correct.
Data() interface{} // Data returns the original representation of the Value
Dtype() tensor.Dtype // Dtype returns the Dtype of the value
tensor.Memory
fmt.Formatter
}
Value represents a value that Gorgonia accepts. At this point it is implemented by:
- all scalar value types (F64, F32... etc)
- *tensor.Dense
- *dualValue
A Value is essentially any thing that knows its own type and shape. Most importantly though, a Value is a pointer - and can be converted into a tensor.Memory. This is done for the sake of interoperability with external devices like cgo or CUDA or OpenCL. This also means for the most part most Values will be allocated on the heap. There are some performance tradeoffs made in this decision, but ultimately this is better than having to manually manage blocks of memory
func CloneValue ¶
CloneValue clones a value. For scalars, since Go copies scalars, it returns itself
func ScalarAsTensor ¶
ScalarAsTensor returns the tensor representation of a scalar. It is particularly useful as a "reshape" of tensors of sorts
The Value passed in are either Scalar, tensor.Tensor, or *dualValue. Anything else will panic.
type ValueCloser ¶
type ValueCloser interface {
ValueClose(interface{}) bool
}
ValueCloser represents any type that can perform a close-value check
type ValueEqualer ¶
ValueEqualer represents any type that can perform a equal value check
type ValueGrad ¶
ValueGrad is any type that has a value and a grad. This is used for Solvers
func NodesToValueGrads ¶
NodesToValueGrads is a utility function that converts a Nodes to a slice of ValueGrad for the solvers
type VanillaSolver ¶
type VanillaSolver struct {
// contains filtered or unexported fields
}
VanillaSolver is your bog standard stochastic gradient descent optimizer. There are no fancy features to this
func NewVanillaSolver ¶
func NewVanillaSolver(opts ...SolverOpt) *VanillaSolver
NewVanillaSolver creates a new VanillaSolver with sane-ish default values
func (*VanillaSolver) Step ¶
func (s *VanillaSolver) Step(model []ValueGrad) (err error)
Step steps through each node in the model and applies the most basic gradient descent algorithm on the value.
This function will error out if the nodes do not have an associated Grad value.
type ZeroValuer ¶
ZeroValuer is a a Value that can provide the zero-value of its type
 Source Files
¶
Source Files
¶
- analysis.go
- api_gen.go
- batch.go
- bitmap.go
- blas.go
- broadcast.go
- collections.go
- compile.go
- const.go
- device.go
- differentiation.go
- doc.go
- dual.go
- engine.go
- equalities.go
- ermagerdmonards.go
- errors.go
- execution.go
- formatter.go
- gorgonia.go
- graph.go
- interfaces.go
- math.go
- math_nooptim.go
- mathutils_amd64.go
- nn.go
- node.go
- node_set.go
- noextern.go
- op.go
- op_infidel.go
- op_math.go
- op_math_noextern.go
- op_nn.go
- op_reduction.go
- op_tensor.go
- operations.go
- operatorLinAlg.go
- operatorLinAlg_const.go
- operatorPointwise_binary.go
- operatorPointwise_binary_const.go
- operatorPointwise_unary.go
- operatorPointwise_unary_const.go
- operatorPointwise_unary_gen.go
- opt.go
- perf.go
- regalloc.go
- release.go
- shape.go
- slice.go
- solvers.go
- stabilization.go
- templates.go
- type.go
- typeSystem.go
- utils.go
- values.go
- values_primitives.go
- values_utils.go
- vm.go
- vm_genera.go
- vm_genera_nocuda.go
- vm_tape.go
- vm_tape_nocuda.go
- walker.go
- weights.go
 Directories
¶
Directories
¶
| Path | Synopsis |
|---|---|
|
Package blase is a thin wrapper over Gonum's BLAS interface that provides a queue so that cgo calls are batched.
|
Package blase is a thin wrapper over Gonum's BLAS interface that provides a queue so that cgo calls are batched. |
|
cmd
|
|
|
encoding
|
|
|
dot
Package dot creates a graphviz compatible version of the ExprGraph
|
Package dot creates a graphviz compatible version of the ExprGraph |
|
examples
|
|
|
mnist
package mnist handles the mnist data set
|
package mnist handles the mnist data set |
|
internal
|
|
|
ops
|
|
|
nn
Package nnops implements some operators that have both a pure go implementation and a cuda implementation to use the cuda version, assuming that you have the pre-requisites, simply compile or run the code with the `cuda tag` go run -tags='cuda'
|
Package nnops implements some operators that have both a pure go implementation and a cuda implementation to use the cuda version, assuming that you have the pre-requisites, simply compile or run the code with the `cuda tag` go run -tags='cuda' |
|
x
|
|