leetcode

README

1579. Remove Max Number of Edges to Keep Graph Fully Traversable

题目

Alice and Bob have an undirected graph of n nodes and 3 types of edges:

• Type 1: Can be traversed by Alice only.
• Type 2: Can be traversed by Bob only.
• Type 3: Can by traversed by both Alice and Bob.

Given an array edges where edges[i] = [typei, ui, vi] represents a bidirectional edge of type typei between nodes ui and vi, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.

Return the maximum number of edges you can remove, or return -1 if it's impossible for the graph to be fully traversed by Alice and Bob.

Example 1:

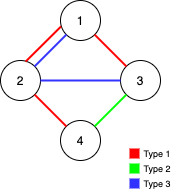
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
Output: 2
Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.

Example 2:

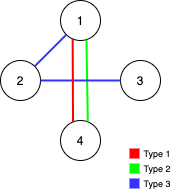
Input: n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
Output: 0
Explanation: Notice that removing any edge will not make the graph fully traversable by Alice and Bob.

Example 3:

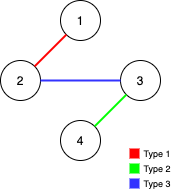
Input: n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
Output: -1
Explanation: In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.

Constraints:

• 1 <= n <= 10^5
• 1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
• edges[i].length == 3
• 1 <= edges[i][0] <= 3
• 1 <= edges[i][1] < edges[i][2] <= n
• All tuples (typei, ui, vi) are distinct.

题目大意

Alice 和 Bob 共有一个无向图，其中包含 n 个节点和 3  种类型的边：

• 类型 1：只能由 Alice 遍历。
• 类型 2：只能由 Bob 遍历。
• 类型 3：Alice 和 Bob 都可以遍历。

给你一个数组 edges ，其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下，找出可以删除的最大边数。如果从任何节点开始，Alice 和 Bob 都可以到达所有其他节点，则认为图是可以完全遍历的。返回可以删除的最大边数，如果 Alice 和 Bob 无法完全遍历图，则返回 -1 。

解题思路

• 本题是第 1319 题的加强版。在第 1319 题中只有一个人，同样也是判断在保证图可连通的基础上，删掉最多边的条数。这一题只不过变成了 2 个人。解题思路依旧是并查集。
• 初始化 2 个并查集，分别表示 Alice 和 Bob。先合并公共边，每合并一条边，可删除的最大总边数便减少 1 。再合并 2 人各自的单独的边，同样是每合并一条边，每合并一条边，可删除的最大总边数便减少 1 。合并完所有的边，2 人的并查集内部集合数仍大于 1，那么则代表 2 人无法完全遍历图，则输出 -1。如果 2 人的并查集内部集合都是 1，代表整个图都连通了。输出可以删除的最大边数。

代码

package leetcode

import (
	"github.com/halfrost/LeetCode-Go/template"
)

func maxNumEdgesToRemove(n int, edges [][]int) int {
	alice, bob, res := template.UnionFind{}, template.UnionFind{}, len(edges)
	alice.Init(n)
	bob.Init(n)
	for _, e := range edges {
		x, y := e[1]-1, e[2]-1
		if e[0] == 3 && (!(alice.Find(x) == alice.Find(y)) || !(bob.Find(x) == bob.Find(y))) {
			alice.Union(x, y)
			bob.Union(x, y)
			res--
		}
	}
	ufs := [2]*template.UnionFind{&alice, &bob}
	for _, e := range edges {
		if tp := e[0]; tp < 3 && !(ufs[tp-1].Find(e[1]-1) == ufs[tp-1].Find(e[2]-1)) {
			ufs[tp-1].Union(e[1]-1, e[2]-1)
			res--
		}
	}
	if alice.TotalCount() > 1 || bob.TotalCount() > 1 {
		return -1
	}
	return res
}