leetcode

README

1353. Maximum Number of Events That Can Be Attended

题目

Given an array of events where events[i] = [startDayi, endDayi]. Every event i starts at startDayi and ends at endDayi.

You can attend an event i at any day d where startTimei <= d <= endTimei. Notice that you can only attend one event at any time d.

Return the maximum number of events you can attend.

Example 1:

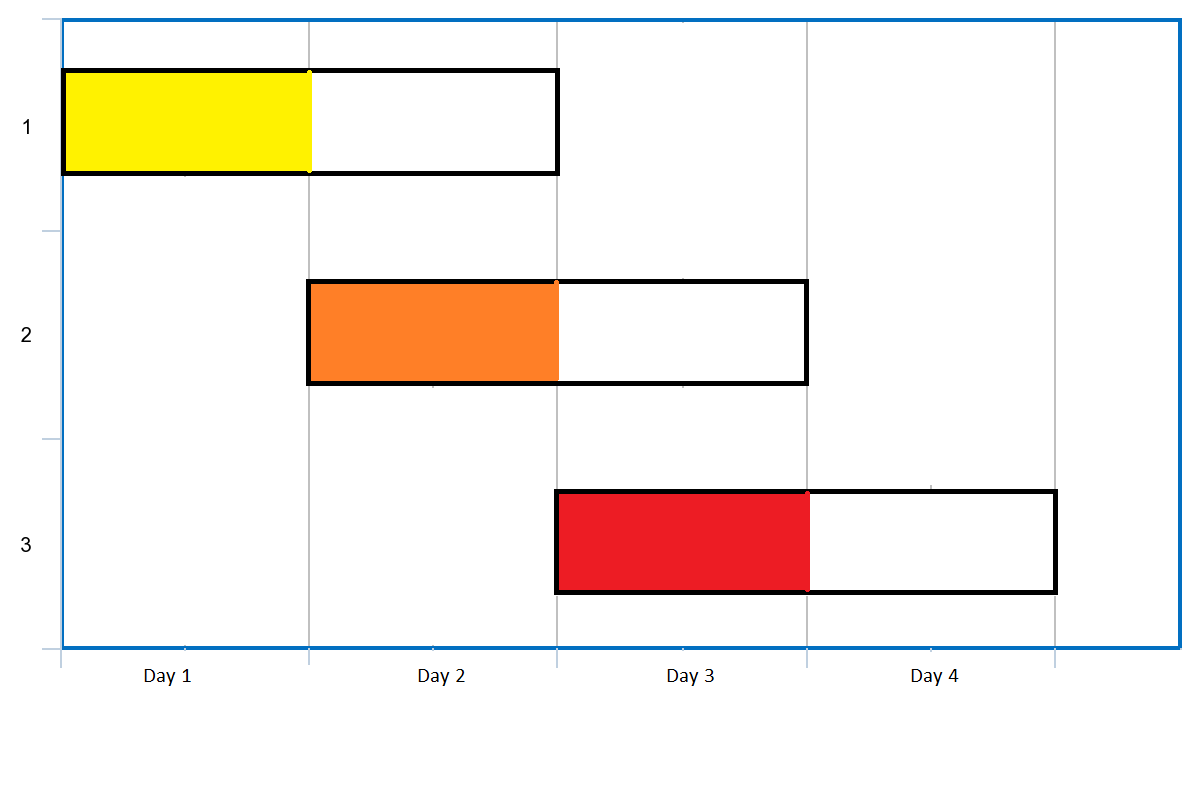
Input: events = [[1,2],[2,3],[3,4]]
Output: 3
Explanation: You can attend all the three events.
One way to attend them all is as shown.
Attend the first event on day 1.
Attend the second event on day 2.
Attend the third event on day 3.

Example 2:

Input: events= [[1,2],[2,3],[3,4],[1,2]]
Output: 4

Example 3:

Input: events = [[1,4],[4,4],[2,2],[3,4],[1,1]]
Output: 4

Example 4:

Input: events = [[1,100000]]
Output: 1

Example 5:

Input: events = [[1,1],[1,2],[1,3],[1,4],[1,5],[1,6],[1,7]]
Output: 7

Constraints:

• 1 <= events.length <= 10^5
• events[i].length == 2
• 1 <= startDayi <= endDayi <= 10^5

题目大意

给你一个数组 events，其中 events[i] = [startDayi, endDayi] ，表示会议 i 开始于 startDayi ，结束于 endDayi 。你可以在满足 startDayi <= d <= endDayi 中的任意一天 d 参加会议 i 。注意，一天只能参加一个会议。请你返回你可以参加的 最大 会议数目。

解题思路

• 关于会议安排，活动安排这类题，第一直觉是贪心问题。先按照会议开始时间从小到大排序，如果开始时间相同，再按照结束时间从小到大排序。贪心策略是，优先选择参加早结束的会议。因为一个结束时间晚的会议，代表这个会议持续时间长，先参加马上要结束的会议，这样可以参加更多的会议。
• 注意题目给的数据代表的是天数。比较大小的时候最好转换成坐标轴上的坐标点。例如 [1,2] 代表这个会议持续 2 天，如果在坐标轴上表示，是 [0,2]，0-1 表示第一天，1-2 表示第二天。所以比较会议时需要把开始时间减一。选定了这个会议以后记得要把这一天排除，例如选择了第二天，那么下次对比起始时间需要从坐标 2 开始，因为第二天的时间范围是 1-2，所以下一轮比较会议前需要把开始时间加一。从左往右依次扫描各个会议时间段，选择结束时间大于起始时间的会议，不断累加次数，扫描完所有会议，最终结果即为可参加的最大会议数。
• 测试数据中有一组很恶心的数据，见 test 文件中最后一组数据。这组数据在同一天叠加了多个会议，并且起始时间完全一致。这种特殊情况需要加判断条件排除，见下面代码 continue 条件。

代码

package leetcode

import (
	"sort"
)

func maxEvents(events [][]int) int {
	sort.Slice(events, func(i, j int) bool {
		if events[i][0] == events[j][0] {
			return events[i][1] < events[j][1]
		}
		return events[i][0] < events[j][0]
	})
	attended, current := 1, events[0]
	for i := 1; i < len(events); i++ {
		prev, event := events[i-1], events[i]
		if event[0] == prev[0] && event[1] == prev[1] && event[1] == event[0] {
			continue
		}
		start, end := max(current[0], event[0]-1), max(current[1], event[1])
		if end-start > 0 {
			current[0] = start + 1
			current[1] = end
			attended++
		}
	}
	return attended
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}