题目
We run a preorder depth first search on the root of a binary tree.
At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node. (If the depth of a node is D, the depth of its immediate child is D+1. The depth of the root node is 0.)
If a node has only one child, that child is guaranteed to be the left child.
Given the output S of this traversal, recover the tree and return its root.
Example 1:
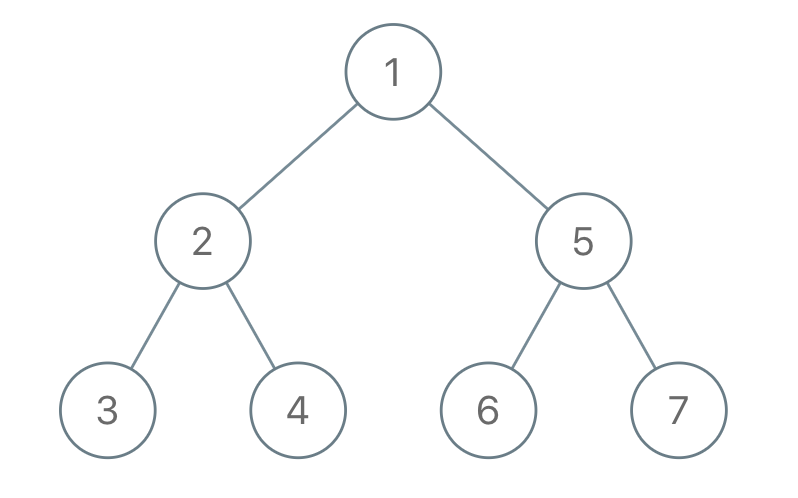
Input: "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]
Example 2:
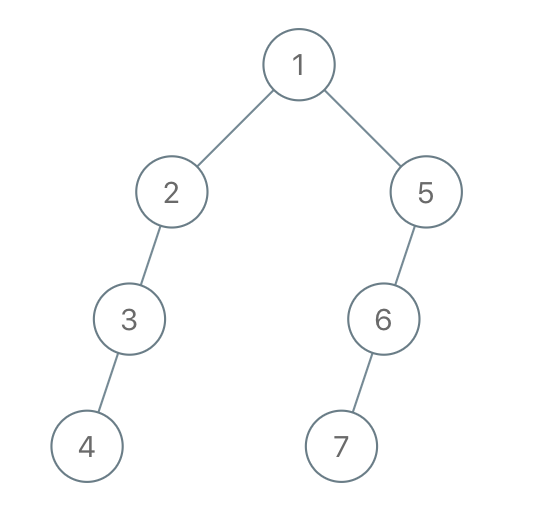
Input: "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]
Example 3:
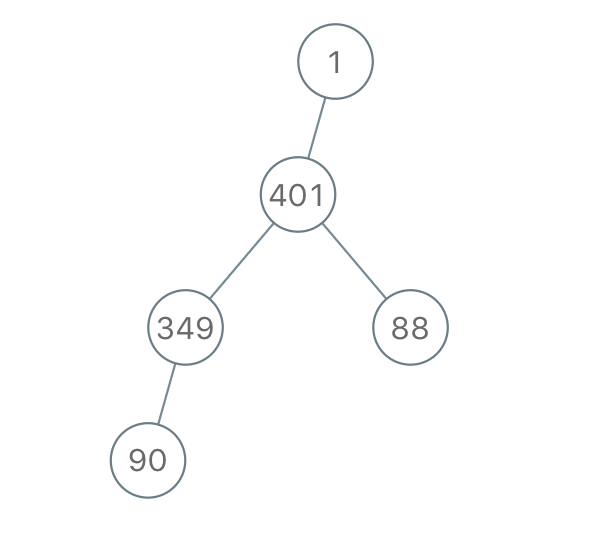
Input: "1-401--349---90--88"
Output: [1,401,null,349,88,90]
Note:
- The number of nodes in the original tree is between
1 and 1000.
- Each node will have a value between
1 and 10^9.
题目大意
我们从二叉树的根节点 root 开始进行深度优先搜索。
在遍历中的每个节点处,我们输出 D 条短划线(其中 D 是该节点的深度),然后输出该节点的值。(如果节点的深度为 D,则其直接子节点的深度为 D + 1。根节点的深度为 0)。如果节点只有一个子节点,那么保证该子节点为左子节点。给出遍历输出 S,还原树并返回其根节点 root。
提示:
- 原始树中的节点数介于 1 和 1000 之间。
- 每个节点的值介于 1 和 10 ^ 9 之间。
解题思路
- 给出一个字符串,字符串是一个树的先根遍历的结果,其中破折号的个数代表层数。请根据这个字符串生成对应的树。
- 这一题解题思路比较明确,用 DFS 就可以解题。边深搜字符串,边根据破折号的个数判断当前节点是否属于本层。如果不属于本层,回溯到之前的根节点,添加叶子节点以后再继续深搜。需要注意的是每次深搜时,扫描字符串的 index 需要一直保留,回溯也需要用到这个 index。