leetcode

README

872. Leaf-Similar Trees

题目

Consider all the leaves of a binary tree. From left to right order, the values of those leaves form a leaf value sequence.

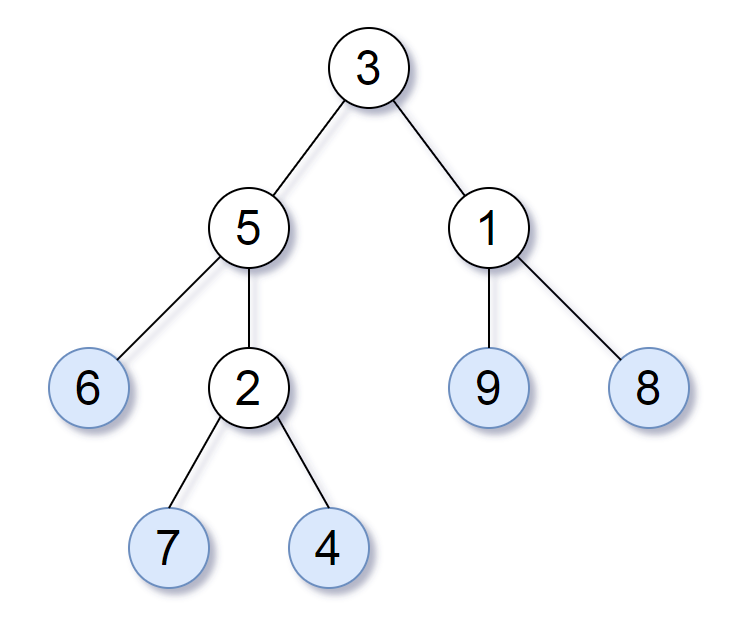
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).

Two binary trees are considered leaf-similar if their leaf value sequence is the same.

Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.

Note:

• Both of the given trees will have between 1 and 100 nodes.

题目大意

请考虑一颗二叉树上所有的叶子，这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。举个例子，如上图所示，给定一颗叶值序列为 (6, 7, 4, 9, 8) 的树。如果有两颗二叉树的叶值序列是相同，那么我们就认为它们是 叶相似 的。如果给定的两个头结点分别为 root1 和 root2 的树是叶相似的，则返回 true；否则返回 false 。

提示：

• 给定的两颗树可能会有 1 到 200 个结点。
• 给定的两颗树上的值介于 0 到 200 之间。

解题思路

• 给出 2 棵树，如果 2 棵树的叶子节点组成的数组是完全一样的，那么就认为这 2 棵树是“叶子相似”的。给出任何 2 棵树判断这 2 棵树是否是“叶子相似”的。
• 简单题，分别 DFS 遍历 2 棵树，把叶子节点都遍历出来，然后分别比较叶子节点组成的数组是否完全一致即可。

代码

func leafSimilar(root1 *TreeNode, root2 *TreeNode) bool {
	leaf1, leaf2 := []int{}, []int{}
	dfsLeaf(root1, &leaf1)
	dfsLeaf(root2, &leaf2)
	if len(leaf1) != len(leaf2) {
		return false
	}
	for i := range leaf1 {
		if leaf1[i] != leaf2[i] {
			return false
		}
	}
	return true
}

func dfsLeaf(root *TreeNode, leaf *[]int) {
	if root != nil {
		if root.Left == nil && root.Right == nil {
			*leaf = append(*leaf, root.Val)
		}
		dfsLeaf(root.Left, leaf)
		dfsLeaf(root.Right, leaf)
	}
}

Documentation

Index

• type TreeNode

Types

type TreeNode

type TreeNode = structures.TreeNode

TreeNode define